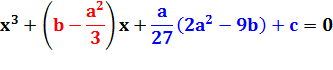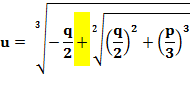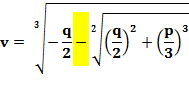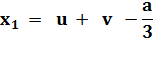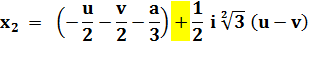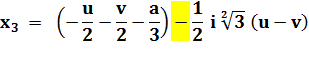NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/03/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	ÉQUATIONS
Débutants Équations	Troisième degré				Glossaire Équations
INDEX Équations	Théorie	Exemple 1	Méthode	Historique
	Factorisation	Exemple 2	Exemple 3	Symétrie
	Nombre d'argent
		Sommaire de cette page >>> Méthode >>> Autre exemples >>> Calcul sur tableur

RÉSOLUTION PRATIQUE

des équations du troisième degré

(équations cubiques)

Méthode dite de Cardan-Tartaglia

et exemples

Formules de résolution – Rappel

Anglais: the formula to solve cubic equations

Je souhaite disposer tout de suite de la solution par tableur >>>

Méthode avec exemple numérique
Équation	x^3  + a.x^2  + b.x + c = 0	x^3 – 2x² + 4x – 8 = 0
Changement de variable	X = x + a/3	X = x – 2/3
Nouvelle équation	X^3 + pX + q = 0	(X + 2/3)^3 – 2(X + 2/3)² + 4(X + 2/3) – 8 = 0 X^3 + 8/3X – 160/27 = 0
Changement de variable	X = u + v u^3 + v^3 + (3uv+p)(u+v)+q = 0	X = u + v u^3+ v^3+ (3uv + 8/3)(u+v) – 160/27 = 0
Condition Ou aussi	3uv + p = 0 uv = –p/3	3uv + 8/3 = 0
Nouvelle équation	u^3  +  v^3  + q = 0	u^3+ v^3– 160/27 = 0
Reprenons les deux équations	u^3 . v^3 = –p^3/27 u^3  +  v^3  + q = 0	u^3 . v^3= –512/729 u^3+ v^3 = 160/27
Solution somme/produit	y² + qy – p^3/27 = 0	y² – 160/27y – 512/729 = 0
Résolution: discriminant		37,925…
Résolution: solutions		u^3 = 6,042… v^3 = –0,116…
Avec les relations initiales	X = u + v	X = 1,821… – 0,488… = 1,333…
Finalement	X = x + a/3	Solution réelle unique x = 2 Solutions imaginaires x = + 2i et x = – 2i

Autres exemples
Équation	x^3– 2x² + 4x – 3 = 0	x^3 – 4x² + 4x – 3 = 0
Changement de variable	X = x – 2/3	X = x – 4/3
Nouvelle équation	(X+2/3)^3– 2(X+2/3)²+4(X + 2/3)–3 = 0 X^3+ 8/3X – 25/27 = 0	(X+4/3)^3–4(X+4/3)²+4(X+ /3)–3 = 0 X^3– 4/3X – 65/27 = 0
Changement de variable	X = u + v u^3+v^3+(3uv+8/3)(u+v) – 25/27 = 0	X = u + v u^3+v^3+(3uv–4/3)(u+v)–65/27 = 0
Condition	3uv + 8/3 = 0	3uv – 4/3 = 0
Nouvelle équation	u^3+ v^3– 25/27 = 0	u^3 + v^3– 65/27 = 0
Reprenons les deux équations	u^3 . v^3 = –512/729 u^3 +v^3 = 25/27	u^3 . v^3= 64/729 u^3+ v^3= 65/27
Solution somme/produit	y² – 25/27y – 512/729 = 0	y² – 65/27y + 64/729 = 0
Résolution: discriminant	3.666…	5,444…
Résolution: solutions	u^3 = 1,420… v^3 = –0,494…	u^3= 2,370… v^3= 0,037…
Avec les relations initiales	X = 1,124… – 0,790… = 0,333…	X = 1,333… + 0,333… = 1,666…
Solution finale	x = 1 Solution unique	x = 3 Solution unique

Équation	x^3+ 2x² + 2x + 2 = 0	X^3 + x² + x – 1 = 0
Changement de variable	X = x + 2/3	X = x + 1/3
Nouvelle équation	(X–2/3)^3+2(X–2/3)²+2(X–2/3)+2 = 0 X^3 + 2/3X + 34/27 = 0	(X–1/3)^3+(X–1/3)²+(X–1/3)–1 = 0 X^3 + 2/3X – 34/27 = 0
Changement de variable	X = u + v u^3+v^3+(3uv + 2/3)(u+v)+ 34/27 = 0	X = u + v u^3+v^3+(3uv+2/3)(u+v)–34/27 = 0
Condition	3uv + 2/3 = 0	3uv + 2/3 = 0
Nouvelle équation	u^3+ v^3 + 34/27 = 0	u^3+v^3– 34/27 = 0
Reprenons les deux équations	u^3 . v^3= –8/729 u^3+v^3= –34/27	u^3. v^3= –8/729 u^3+v^3 = 34/27
Solution somme/produit	y² + 34/27y – 8/729 = 0	y² – 34/27y – 8/729 = 0
Résolution: discriminant	1,629…	1,629…
Résolution: solutions	u^3= 0,0086… v^3= –1,2679…	u^3 = 1,2679… v^3 = –0,0086…
Avec les relations initiales	X = 0,205…– 1,082… = –0,877…	X = 1,0823… – 0,205… = 0,877…
Solution finale	x = –1,543… Solution unique	x = 0,543… Solution unique

CALCUL SUR TABLEUR (Excel)

Résolution équation du 3e degré – Formule de calcul

	A	B	C	D	E	F	G
1
2		Équation
3		X^3	+a X^2	+b X	+ c	= 0
4		Coefficients =>	-2	4	-8
5		Calculs
6	p	q
7	=D4-(C4^2/3)	=C4/27*(2*C4^2-9*D4)+E4	R
8			=1/2*((4*A7^3+27*B7^2)/27)^(1/2)	X1	X2
9				=(-B7/2+C8)^(1/3)	=(-B7/2-C8)^(1/3)	X
10						=D9+E9	x
11							=F10-C4/3

Faire simplement un copier – coller de ces cellules au même endroit (de A1 à G11) dans une feuille de calcul Excel.

Exemple d'exécution

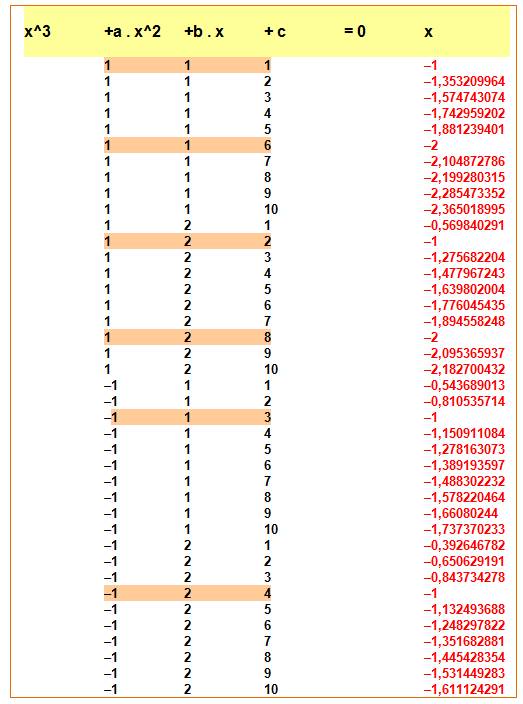
Exemples de calculs systématiques

Voir Programmation

Suite	Résolution des équations du 3^e degré Autres pages sur 3^e degré Résolution symétrique de Lagrange
Voir	Algorithme d'Héron Équation de Pell Méthode de Newton Système d'équations particulier
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Eqa3dres.htm