|
|||||||||||||||||||||||||||||||||||
![]()
|
Nombre – Vocabulaire de base Voici quelques définitions
qui se veulent le plus possible abordables par le novice, avec des
explications volontairement approximatives, mais justes. La précision et la
prise en compte des particularités viendront avec l'expérience dans ce
domaine. En jaune, ceux à connaître
absolument! |
|
ASSOCIATIVITÉ |
Propriété
qui permet des remplacements de valeurs sans changer le résultat.
2 + (3 + 4) = 2 +
7 = 9 (2 + 3) + 4 = 5 +
4 = 9
2
x (3 x 4)
= 2 x 12 = 24 (2
x 3) x 4 = 6 x 4 = 24 Attention, cette propriété ne vaut que si l'on reste dans le même monde des
additions ou des multiplications, et non pas si les deux sont mélangées. |
|
|
BIT |
Il
nous faut neuf chiffres pour compter (0, 1, …, 9). Les ordinateurs en en
utilisent seulement deux (0 et 1). Ils comptent: 0, 1, 10, 11, 100, 101 … Évidement cela donne vite de très grands nombres. Mais les ordinateurs savent gérer ces monstres. Le
chiffre binaire s'appelle bit. Le nombre binaire de l'exemple comporte 17 bits. Bit est une abréviation de binary
digit (traduction de chiffre binaire) |
|
|
BYTE |
Mot
anglais pour octet, un nombre binaire de 8 bits. un kilooctet se dit kilobyte
et vaut 1024 bits. |
|
|
CARDINAL (voir ordinal) |
Nombre
exprimant une quantité Il
y a 32 cartes dans un jeu ordinaire de cartes: 32 est le cardinal du jeu de
cartes. Une
collection, un ensemble comporte cinq éléments, son cardinal est 5. |
|
|
CHIFFRE |
Chacun
des 10 symboles qui servent à compter: 0,
1, 2, 3, 4, 5, 6, 7, 8 et 9 |
|
|
COLLECTION (voir ensemble) |
Rassemblement,
regroupement d'objet. Famille
d'objets quelle que soit la quantité d'exemplaires de chacun. |
|
|
COMMUTATIVITÉ |
Propriété
d'une opération dans laquelle on peut inverser l'ordre des termes.
|
|
|
DÉCIMAL |
Nombre
décimal: nombre avec des chiffres derrière la virgule. Exemple:
12,345 ou 3/8 = 0,375. Mais
1/3 = 0,333 … est périodique et non décimal. Système
décimal: notre manière de compter avec 10 chiffres. Nous comptons presque toujours par 10. Parfois par 60 pour les minutes et les secondes. |
||
|
DÉNOMINATEUR |
Partie
inférieure d'une fraction.
Il détermine en combien de part on "découpe
le gâteau". C'est le dénominateur qui caractérise la taille des parts. Attention: les opérations avec les fractions ne sont possibles que si les
tailles des parts sont les mêmes. |
||
|
DIGIT |
Le
mot anglais pour dire chiffres. Parfois
utilisé en français (informatique): un nombre à 3 chiffres ou à 3 digits. Digital est le mot anglais pour numérique. Digit vient de doigt. |
||
|
DISTRIBUTIVITÉ |
Propriété
qui permet d'effectuer des calculs en présence d'addition et de
multiplication – Opération inverse de la mise en facteur
|
|
|
|
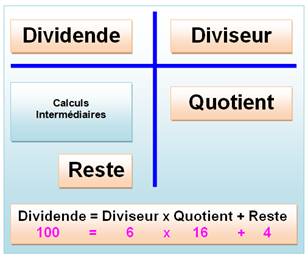
DIVIDENDE DIVISEUR |
Nombre
que l'on cherche à diviser. Nombre
qui divise un nombre- Diviseurs de 12: 1, 2, 3, 4, 6, 12 |
|
|
|
Nom
générique de chacun des individus d'une collection, d'un ensemble
|
|
||
|
ENSEMBLE |
Collection
d'objets uniques, baptisés "éléments". Contrairement à la collection, un objet n'est
présent qu'une seule fois au plus. |
Exemple
avec l'ensemble des quatre couleurs aux cartes.
|
|
|
ENTIER |
Les
nombres entiers servent à compter les objets. Ce sont les nombres usuels, ceux sans chiffre
derrière la virgule. |
||
|
FACTEUR (voir diviseur) |
Nombre
premier qui divise un nombre. Les
facteurs de 12 sont: 2 et 3. Les
nombre 4 et 6 sont des diviseurs de 12, pas des facteurs. Dans
une multiplication, les nombres à multiplier sont des facteurs. 12
x 34 x 56 = 22 848; les nombres 12, 34 et 56 sont les facteurs et 22 848 le
produit. Un
nombre qui multiplie une somme est mis en facteur commun. 5
(6 + 7 + 8 + 9) = 150; le nombre 5 est un facteur commun des nombres 6, 7, 8
et 9. Cette écriture est une façon abrégée d'écrire: 5x6 + 5x7 + 5x8 + 5x9 =
30 + 35 + 40 + 45 = 150. |
||
|
FRACTION (voir numérateur, dénominateur) |
Division
non effectuée de deux nombres. Exemples:
|
||
|
GROUPE |
Ensemble
doué d'un groupe de propriétés particulières
|
||
|
INFINI |
Nombre
encore plus grand que le plus grand que l'on puisse imaginer. Il
y a une infinité de:
|
|
|
MISE EN FACTEUR |
Opération
qui consiste à isoler une fois pour toute une quantité qui revient plusieurs
fois dans une opération - Opération
inverse de la distributivité.
|
|
|
NOMBRE |
Formé
de chiffres, le nombre sert à compter: 11, 12, 13, 14, 15 … |
|
|
NUMÉRATEUR (voir dénominateur) |
Partie
supérieure d'une fraction Le gâteau étant divisé en parts égales
(dénominateur), le numérateur indique le nombre de parts que je prends. |
|
|
ORDINAL (voir cardinal) |
Nombre
exprimant un ordre de rangement. Il
est arrivé troisième. |
|
|
PARENTHÈSES |
Elles
servent à séparer les opérations. (2
+ 3) x (4
+ 5) = 5 x 9 = 45 (2
x 3) + (4
x 5) = 6 + 20 = 26 Règle: faire les opérations entre parenthèses en premier. |
|
|
PRODUIT (voir facteur) |
Nombre
résultat de la multiplication de nombres. |
|
|
PUISSANCE |
Nombre
qui résulte de la multiplication d'un nombre par lui-même un certain nombre
de fois Un
carré est une puissance 2; un cube est une puissance 3. Exemples:
4² = 4 x 4 = 16; le carré de 4 est 16 45
= 4 x 4 x 4 x 4 x 4 = 1024; la puissance cinquième de 4 est 1024. |
|
QUOTIENT (voir dividende) |
Nombre
résultat de la division de deux nombres. |
|
|
RATIONNEL (voir fraction) |
Nombre
exprimable par une fraction (une ration). Certains
nombres décimaux ne sont pas exprimables par une fraction comme π = 3,
14 … Ce sont des nombres irrationnels |
|
|
RELATIF |
Nombre
accompagné d'un signe + ou – Le
signe plus est très souvent omis (sous-entendu). |
|
|
SOMME |
Nombre
résultat de l'addition de nombres. |
|
|
SYMBOLE |
Convention
d'écriture pour raccourcir les notations
|
|
|
TERME |
Chacune
des quantités que l'on veut additionner. On
parle:
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Debutant/Nombres/Glossair.htm |
![]()