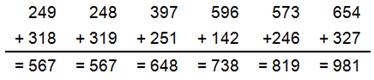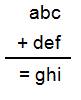|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
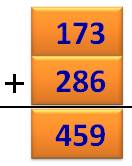
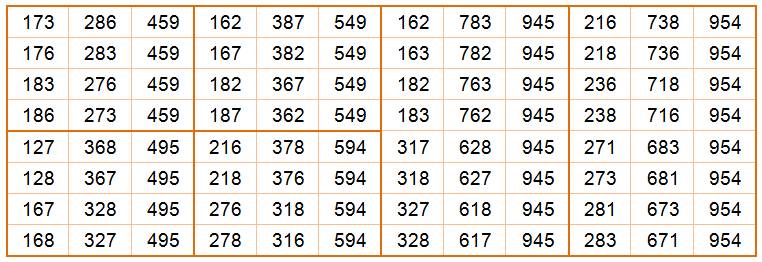
PUZZLES ARITHMÉTIQUES Addition de trois triplets pannumériques
Ajoutez deux
nombres de trois chiffres pour en obtenir un troisième, sachant que tous les chiffres
sont différents. Combien de
solutions? Il y en a 168, y compris les permutations. Occasion d'une
recherche arithmétique digne d'intérêt. |
Anglais: Add two three digit numbers to make a third. The
challenge is to do it using only the digits 1 - 9.
|
|
||
|
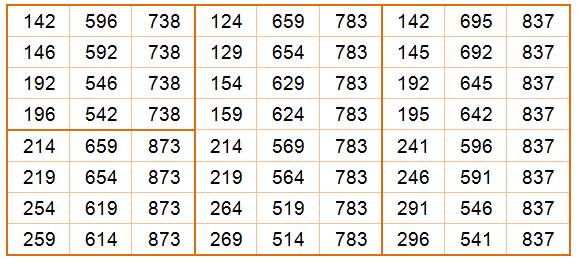
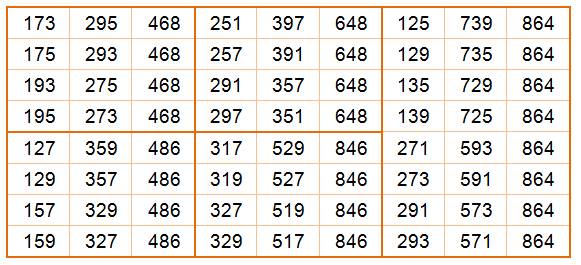
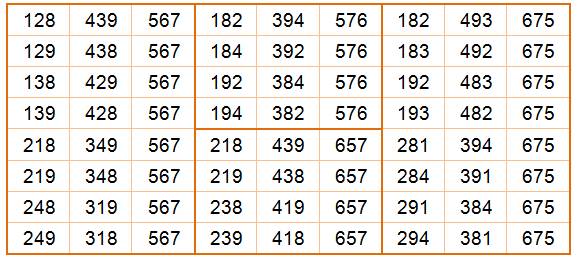
Toutes
ces additions sont pannumériques (tous les chiffres de 1 à 9 sont utilisés). Une
observation attentive du résultat
montre la somme des chiffres est toujours 18. Est-ce une propriété? |
|
|
|
|
|||
|
Chaque
lettre est un chiffre différent. Il y a en neuf comme les neuf chiffres, hors
le 0. À droite,
la démonstration qui montre que l'addition est impossible sans retenue. |
|
a + b + c + d + e + f + g
+ h + i = 45 a + d = g b + e = h c + f = i g + h + i + g + h + i =
45 2 (g + h + I) = 45 Pair = Impair; impossible |
|
|
Supposons
une retenue pour la somme des unités |
a + d = g b + e + 1 = h c + f = 10 + i |
g + h – 1 + 10 + i + g + h + i = 45 2(g + h + i) = 36 g + h + i = 18 |
|
|
Supposons
une retenue pour la somme des dizaines |
a + d + 1 = g b + e = 10 + h c + f = i |
g – 1 + h + 10 + i + g +
h + i = 45 2(g + h + i) = 36 g + h + i = 18 |
|
|
Supposons
une retenue pour la somme des dizaines et celle des unités |
a + d + 1 = g b + e + 1 = 10 + h c + f = 10 + i |
g – 1 + h + 9 + i + 10 +
g + h + i = 45 2(g + h + i) = 45 – 18 =
27 Pair = Impair; impossible |
|
|
Somme de
trois chiffres différents = 18. |
Sept possibilités, plus les permutations |
9 + 8 + 1 = 18 9 + 7 + 2 = 18 9 + 6 + 3 = 18 9 + 5 + 4 = 18 8 + 7 + 3 = 18 8 + 6 + 4 = 18 7 + 6 + 5 = 18 |
|
|
|
|
|
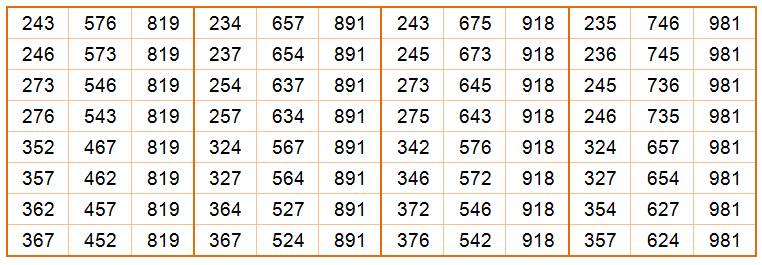
Chacune
de sept sommes offre une panoplie de possibilités par permutation des
chiffres. De sorte que sur 7 modèles de base, on atteint 168 sommes pannumériques. Le
dénombrement n'est pas évident sans les lister toutes. 1,8,9
2,7,9
3,6,9
4,5,9
3,7,8
4,6,8
5,6,7
|
|
![]()
![]()