|
Édition du: 30/01/2022 |
|
INDEX |
Puzzles arithmétiques |
|||
|
Libres (à trous) |
||||
Faites un double-clic pour un retour en haut de page
![]()
|
CRYPTARITHME - Résolution Comment, si
possible, résoudre un cryptarithme réputé très difficile. Plusieurs
possibilités:
Solveur comme
programme-maison peuvent être utilisés pour inventer de nouveaux
cryptarihmes. |
||
|
|
Sommaire de cette page >>> Le cryptarithme casse-tête à résoudre >>> Résolution manuelle / aide tableur >>> Programmation |
Débutants Glossaire |
|
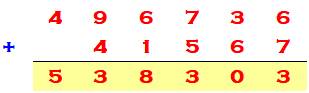
Le puzzle Chaque lettre est à remplacer pour rendre
l'addition exacte. On facilite la recherche de la solution en
précisant que le chiffre 2 n'est pas utilisé. |
|
|
|
Sa solution La vérification par programmation
montre qua la solution est unique, avec ou sans le chiffre 2. |
|
|
|
Correspondance Il faut donc trouver les neuf chiffres rouges
pour remplacer les lettres bleues. |
|
|
|
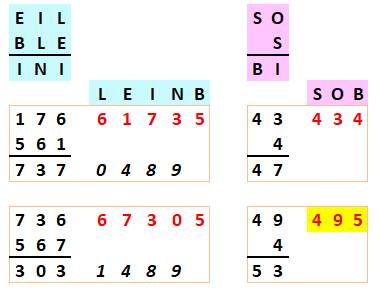
La queue de l'addition Cette configuration sur les trois dernières
colonnes est sympathique ! On peut chercher à mettre ces additions en
équations. Attention à prendre soin des retenues. Même avec cette configuration redondante, il y a trop d'inconnues pour ces trois
équations. Même si r, s et t ne prennent que deux valeurs: 0 ou 1. Avec de la persévérance (beaucoup !), on trouve
huit configurations recevables. Voir Une méthode possible |
L + E = 10r + I
E + B + s = 10t + I Idée: commencer les essais en choississant une valeur
pour I, puis pour E. |
|
|
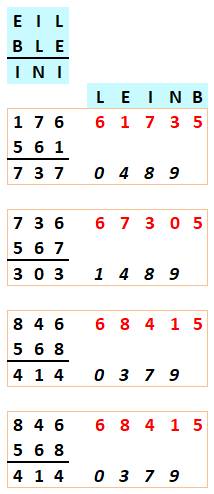
Huit configurations Le
tableur est utilisé comme ardoise intelligente. Pour chaque solution (encadrée):
Remarquez qu'un grand nombre d'additions
comportent des retenues. Ce qui ajoute de la complexité à la recherche. |
|
Exemple de recherche systématique
|
Avec le tableur, les chiffres choisis en rouge
sont automatiquement reportés dans l'addition Au départ, aucun chiffre en rouge: 1.
Choix I = 9, par exemple; 2.
Choix E = 1, par exemple; 3.
Les valeurs suivantes sont déterminées: a.
L = 9 – 1 = 8 b.
N = 9 + 8 => 7 et 1 de retenue c.
B = 9 – 1 – 1 = 7 4.
Choix refusé car le 7 est en double. Avec 9 possibilités pour I et 8 pour E, il faut
explorer 72 cas. |
|
|
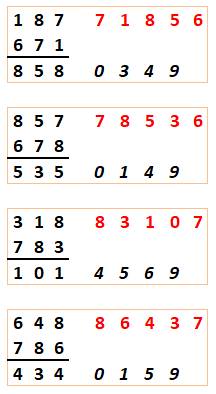
Avec la tête de l'addition À droite cette addition avec les lettres S, O et
B. Elles sont à remplacer par des chiffres parmi ceux en italique. Dans le premier cas (en haut), aucun des chiffres
disponibles ne permet de construire une addition juste. Dans le deuxième cas (en bas), S = 4 et O = 9
permettent de réaliser une addition correcte. |
Cette deuxième configuration est retenue pour
analyse complémentaire. |
|
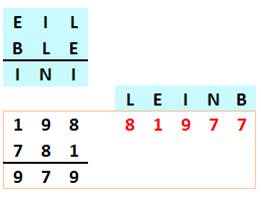
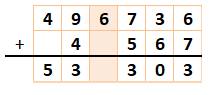
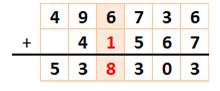
Finalisation La recherche conduit à cette configuration où
seule la colonne ocre est à compléter. Il reste deux chiffres disponibles: 1 et 8. Ça
marche ! |
Solution trouvée ! |
|
But Trouver la solution du cryptarithme en énumérant
les chiffres correspondant aux lettres. |
Principe Balayer systématiquement toutes les lettres. Lorsqu'un chiffre est choisi, il est retiré du
champ des possibles pour la lettre suivante. Les chiffres sélectionnés sont convertis en trois
nombres. La somme des deux premiers est comparée au
troisième. |
||
|
Programme Maple
|
Commentaires Initialisation de l'ensemble de départ avec tous
les chiffres. La lettre S est choisie parmi les neuf possibles
(Set) et l'ensemble Set1 est privé de ce chiffre (minus). Idem pour la suite. La solution (Sol)
est l'énumération des lettres (de droite vers gauche dans l'addition). Si la quantité de chiffres dans la liste [ ] Sol est
la même que dans l'ensemble { } Sol, c'est que les chiffres sont
tous différents, alors on poursuit. Calcul des nombres et, si l'addition est juste,
impression des chiffres trouvés. Avec cette méthode de réduction du champ des possibles, le temps de calcul
est de quelques secondes. |
||
|
restart; Set := {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
for S in Set do Set1 := Set minus {S}; for OO in Set1 do Set2 := Set1 minus
{OO}; for L in Set2 do Set3 := Set2 minus {L}; for E in Set3 do Set4 := Set3
minus {E}; for II in Set4 do Set5 := Set4 minus {II}; for A in Set5 do Set6
:= Set5 minus {A}; for B in Set6 do Set7 := Set6 minus {B}; for K in Set7 do
Set8 := Set7 minus {K}; for N in Set8 do Sol := [S, OO, L, E, II, A, B, K,
N]; if nops(Sol) = nops({op(Sol)}) then a1 :=
S*10^5+OO*10^4+L*10^3+100*E+10*II+L; a2 := S*10^4+A*10^3+100*B+10*L+E; a3 :=
B*10^5+II*10^4+K*10^3+100*II+10*N+II; if a1+a2 = a3 then lprint(S, OO, L, E,
II, A, B, K, N) end if: end if: end do: end do: end do: end do: end do: end
do: end do: end do: end do: |
Code pour copier-coller dans Maple |
||
Voir Programmation – Index
Merci
à Kenzy pour l'idée de cette page
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |