|
||||||||||||||||||||
![]()
|
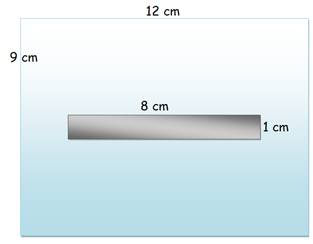
Carrés et rectangles à trou Le problème du tapissier: comment utiliser une moquette
de forme carrée sur une pièce rectangulaire dont le centre, un carré ou un
rectangle, ne doit pas être couvert ? La solution n'est pas banale. Comment
procéder pour y accéder ? |
|
|
||
|
Remarque
Contrainte
Ce problème est
parfois posé en disant qu'un tapissier doit poser une moquette dans une pièce
dont le centre est occupé par une console ou un aquarium. |
|
|
Voir Solution
|
|
|
|
|
|
Voir Solution
|
|
|
|
|
|
|
|
||
|
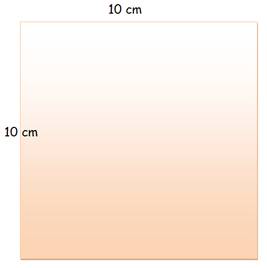
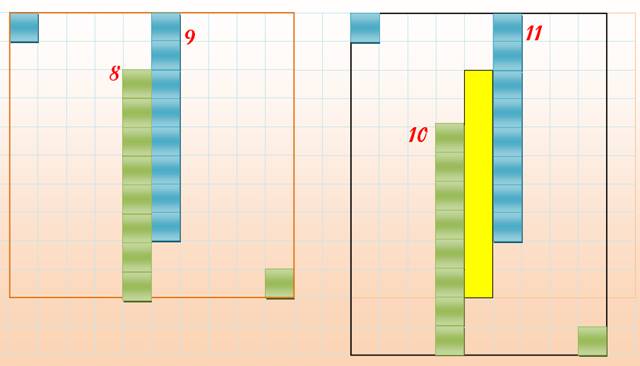
Surface du carré: 6 x 6 = 36
|
|
|
|
|
|
|
|
|
|
de la
solution du 10 x 10 |
|
|
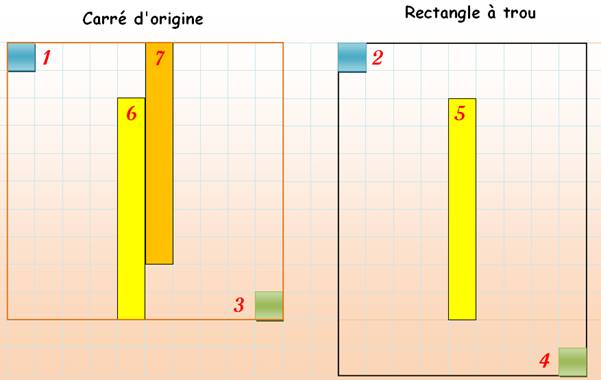
Positions
de chacun des petits carrés
Position
du trou
|
|
|
Solution
du carré 10 x 10 |
|
|
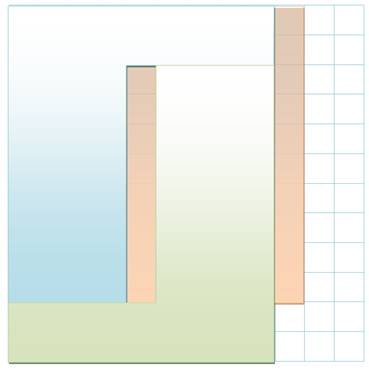
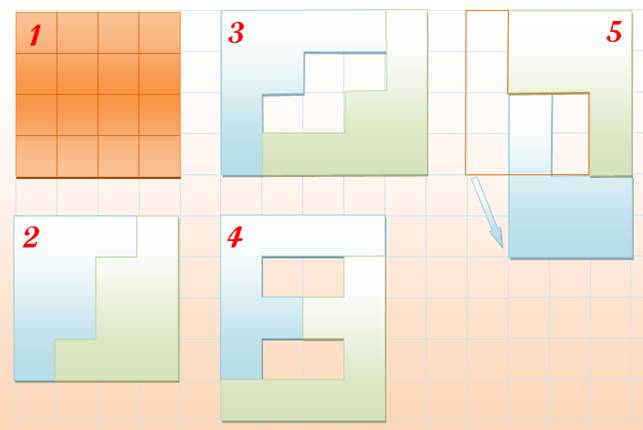
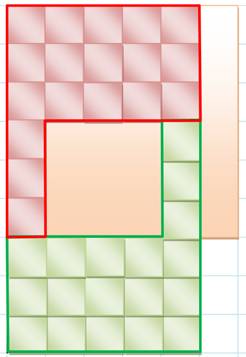
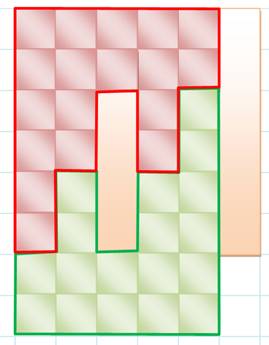
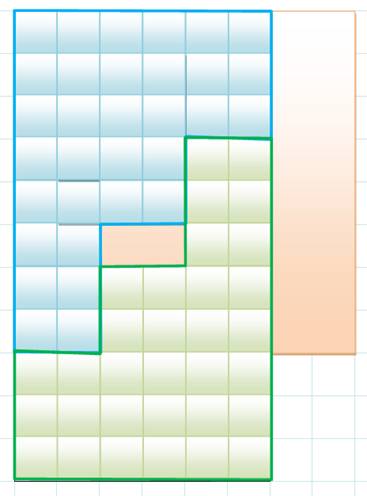
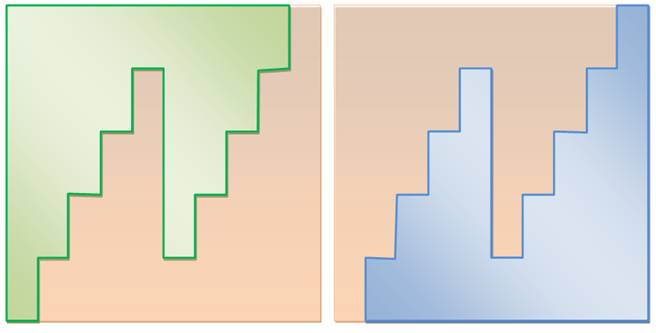
Découpe
du carré en deux pièces, l'une bleu et l'autre verte.
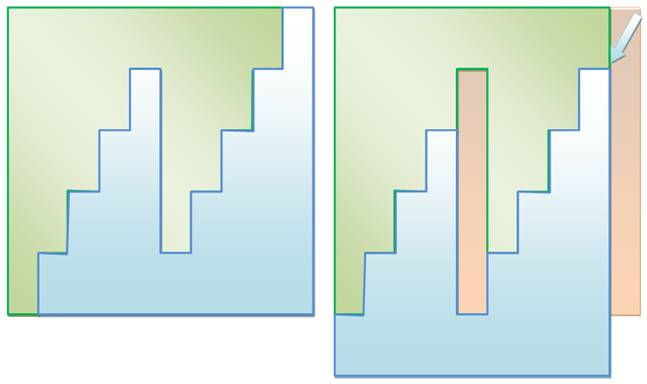
Couverture
du carré avec les deux pièces bleue et verte, et, à droite, glissement de la pièce
verte pour couvrir le rectangle troué
Patron pour réaliser la
découpe du carré
|
|
|
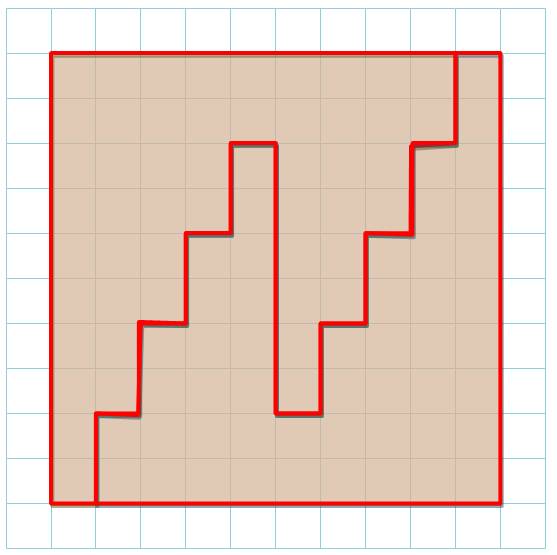
à
partir du carré 10 x 10 |
|
|
14 x 8 – 2 x 6
16 x 7 – 3 x 4 18
x 6 – 2 x 4
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()