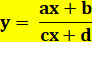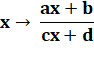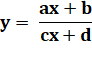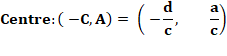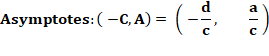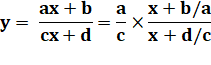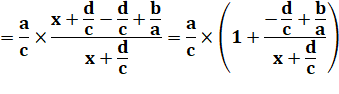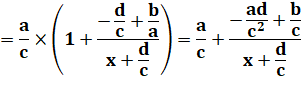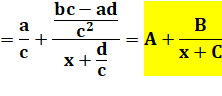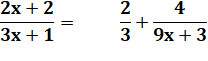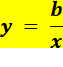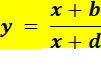|
Édition du: 12/02/2021 |
Pages sur l'hyperbole
![]()
|
Hyperbole homographique La fonction homographique, quotient de deux polynômes du premier degré
a une hyperbole pour graphe.
|
||
|
|
>>> Approche >>> Notations -
Fonction homographique >>> Forme inverse
de x >>> Allure du
graphe de la fonction homographique >>> Hyperbole en
révolution >>> Anglais |
Débutants Glossaire |
|
Fonction homographique Quotient
de deux polynômes du premier degré.
Hyperbole (définit par une
fonction) homographique Graphe de
la fonction homographique:
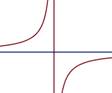
Le graphe* est une hyperbole
équilatère. Si c est nul et d non nul, le graphe est une droite. * le graphe est la courbe représentative dans un
repère orthonormal
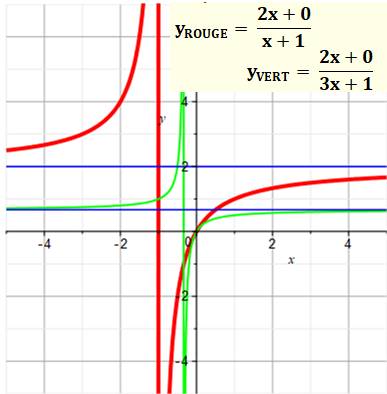
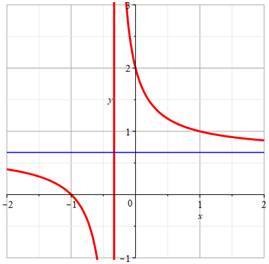
(orthogonal avec vecteurs de même norme (longueur). Asymptotes Les lignes verticales rouge et verte représentent
l'une des asymptotes de la fonction. En ces lieux où le dénominateur
s'annule, la fonction n'est pas
définie. Il y a un "trou": xROUGE = – 1 et xVERT = – 1/3. L'asymptote en horizontal est obtenue pour y
tendant vers l'infini, soit le rapport des coefficients en x: yROUGE
= 2 et yVERT = 2/3. |
Exemple
Asymptote verticale pour dénominateur nul Asymptote horizontale pour y = – a/c. |
|
Notations mathématiques à propos de la fonction
homographique

Voir Fonction inverse et notations / Symboles
mathématiques
|
La fonction homographe peut se
mettre sous la forme d'une fonction "inverse étendue". Une astucieuse manière de calculer
pour isoler la variable x. Paramètres de l'hyperbole
Intérêt Permet
d'étudier la variation de la fonction. |
|
|
|
Exemple
Centre en (-1/3 , 2/3) Asymptote verticale: x = -1/3 Asymptote horizontale: y = 2/3 |
|
|
|
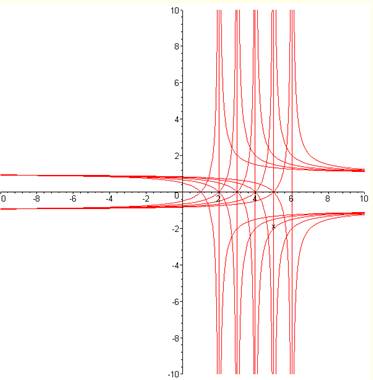
Effet du paramètre b: Le paramètre b vaut successivement: tandis que c = 1 et a et d valent 0.
Note: On a tracé y
et –y pour un effet d'esthétique. |
|
|
|
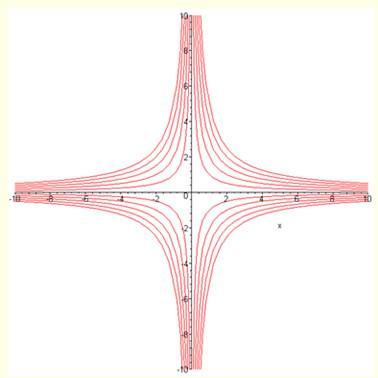
Effet des paramètres b et d: Le paramètre b vaut successivement: Et le paramètre d vaut
successivement: tandis que a = c = 1
Note: On a tracé y et –y pour un effet d'esthétique. |
|
|
|
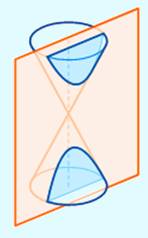
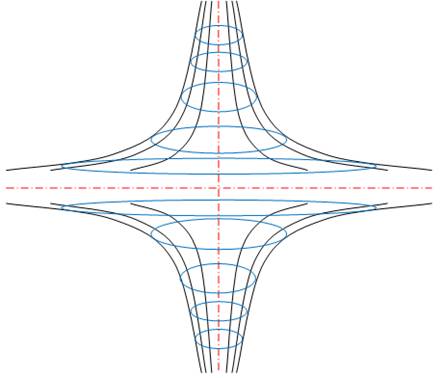
Faisons tourner une hyperbole autour
de son axe vertical. L'intérieur est un volume de
dimension infinie vers le haut, le bas et à l'horizontale. Imaginez deux chapeaux de magicien tête-bêche, dont les pointes
seraient infinies et les rebords infinis également. |
|
|
|
A homographic function is
the quotient of two first-degree polynomial functions through an expression
in the form:
The graphic
representation of a homographic function is an equilateral hyperbola. When c = 0, the function
is reduced to a first-degree polynomial function represented by a line. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/HyperGen.htm
|
|