Théorème de Pythagore, Démonstrations par dissections

Édition du: 09/11/2021

INDEX Triangles Géométrie Opérations sur les puissances	Théorème de Pythagore
	Débutants	Nomenclature – Types de démonstrations		Applications
	Toute figure	Approche	Calcul Aires	Dissections
	Triplets de P.	Historiques	Similitudes	Hypoténuse
	Pappus-Clairaut	Chinoise (Chou Pei)	Algébrique	Pyramide

Démonstrations par dissections du

Théorème de Pythagore

Ces méthodes ne sont pas à proprement parler des démonstrations, mais elles montrent les égalités de surface par déplacement de pièces découpées dans une figure pour en former une autre.

Sommaire de cette page

>>> Dissection découverte

>>> Découpage d'Airy

>>> Démonstration par dissection à deux triangles

>>> Dissection de Dudeney

>>> Démonstration par dissection à quatre triangles

>>> Dissections (puzzle) à sept et huit pièces

Débutants

Géométrie

Glossaire

Géométrie

Voir Types de démonstrations du théorème de Pythagore

Dissections découvertes

haut

Dissection souvent proposée comme activité de découverte du théorème de Pythagore.

Composé à partir du triangle rectangle (3, 4, 5).

Remarquez qu'il suffit de faire glisser les pièces pour former le grand carré à partir des deux plus petits.

Cette nouvelle dissection est attribuée à Liu Hui datant de 300 av. J.-C. (?)

Elle ressemble beaucoup à la précédente; le petit carré est partagé en deux; elle crée un quatrième carré au centre du grand carré.

Découpage d'Airy		haut
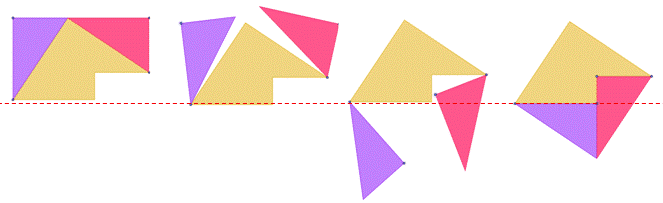
Le montage articulé d'Airy avec les étapes de transformation Explications
La figure en haut à gauche montre deux carrés (moyen et petit; voir la construction ci-contre) qui après mouvements se transforment en un carré plus grand (oblique). La construction est due à l’astronome George Biddle Airy (1801-1892), vers 1855. Les trois pièces peuvent être articulées et faire l'objet d'une réaliation mécanique. La justification sera claire en lisant la suite.	Construction

Voir Puzzle de Gouju par Liu Hui (dissection) / Autres puzzles/dissections / Nomenclature

Preuve animée

enter image description here

Démonstration par dissection à deux triangles

haut

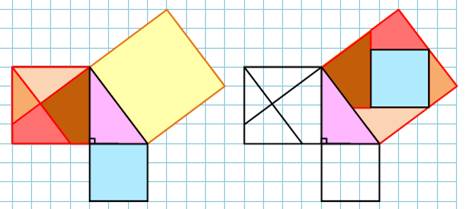
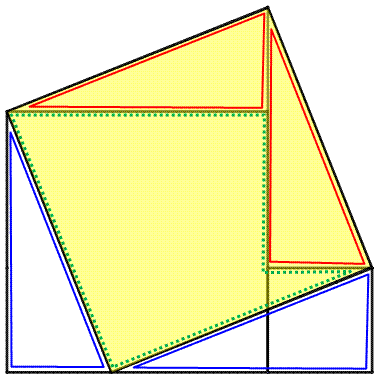
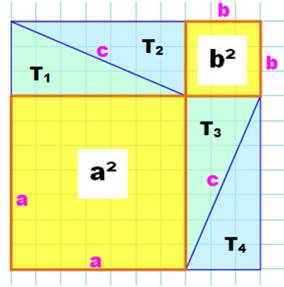
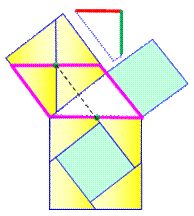
Construction

Triangle rectangle en haut de la figure.

Grand carré sur l'hypoténuse.

Moyen carré sur grand côté.

Petit carré, de la taille du petit côté du triangle, accolé en bas du carré moyen.

Démonstration

Grand carré = VERT + ROUGES

Moyen carré + Petit carré = VERT + BLEUS

Les quatre triangles rectangles étant isométriques:

Grand carré = Moyen carré + Petit carré.

Dissection de Dudeney (1917)

Le grand carré oblique contient le petit carré et peut être complété par les pièces du carré moyen qui débordent.

Henry Dudeney

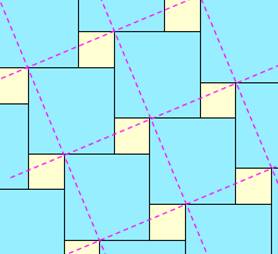
Pavage correspondant

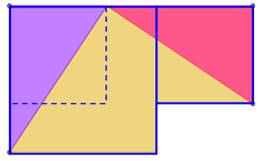
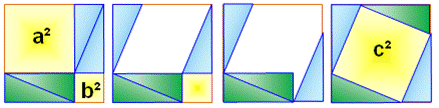
Démonstration par dissection à quatre triangles		haut
Principe: passage de (a² + b²) à c² par simples glissements (translations)
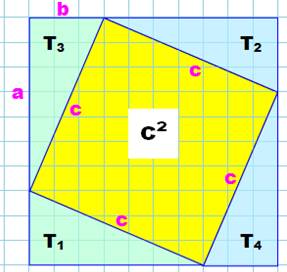
Cas classique de dissection du carré Le premier carré (à gauche) est découpé pour reformer le second (à droite) avec les mêmes pièces. *De chaque grand carré, on retire les quatre triangles identiques. Les surfaces restantes en jaune* sont identiques: a² + b² = c² Explications si nécessaire … En haut, un carré (a + b) découpé en deux carrés (a) et (b) et quatre triangles rectangles égaux (isométriques) dont les dimensions sont a, b et c pour l'hypoténuse. Avec ces pièces, on compose un nouveau carré (en bas) qui a rigoureusement les mêmes dimensions que le premier (a + b). Les triangles rectangles identiques sont plaqués sur les bords du grand carré. 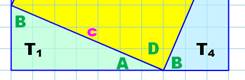La place laissée libre au centre est un quadrilatère dont les quatre côtés sont de longueur c. Pourquoi un carré central En géométrie élémentaire, on apprend que: dans un triangle rectangle, les deux angles non-droits sont complémentaires (= 90°). Sur la figure dans le triangle T₁ : A + B = 90°. Même chose dans le triangle T₄ avec l'angle B. Or les deux triangles T1 et T4 sont alignés par leur côtés; donc: A + D + B = 180°. En rapprochant de l'égalité précédente, on déduit: D = 90° Le quadrilatère a quatre côté égaux (hypoténuse c des triangles rectangles) et un angle droit, c'est un carré.**

Voir Démonstration chinoise / Construction de a² / Dissections

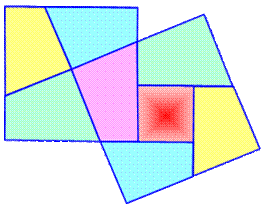
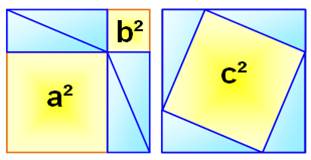
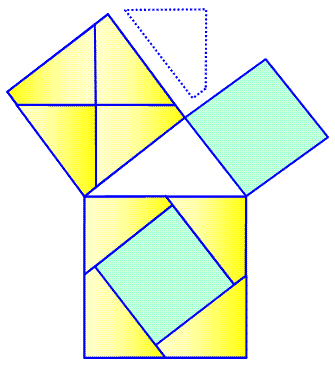
Démonstration par dissection de Perigal

haut

Historique

Henry Perigal (1801-1898) mathématicien amateur britannique auteur de Geometric Dissections and Transpositions (1891)

Dissection en cinq pièces dont quatre identiques (le modèle est montré en encart pointillé).

Il a fait graver cette dissection sur sa tombe.

Dissection

Le carré moyen est découpé en quatre pièces identiques (comme celle montrée en pointillé). Celles-ci sont repositionnées au quatre coins du grand carré.

Le petit carré (bleu) est placé tel quel au centre du grand carré.

Notez que l'on passe des deux carrés du haut à celui du bas par simple glissement (translation) des pièces.

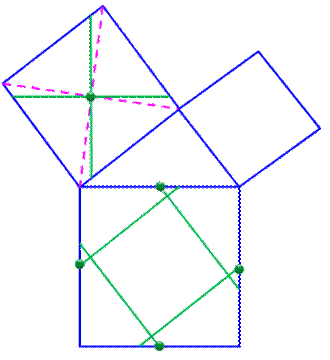
Construction

Centre du carré moyen en traçant les diagonales. Les traits verts sont parallèles à l'hypoténuse du triangle rectangle.

Les quatre pièces apparaissent naturellement.

Milieux des côtés du grand carré (points verts).
Parallèles aux côtés du triangle rectangle.

Les quatre pièces se présentent en gommant le petit segment proche des points verts.

Justification

1) En rose, un parallélogramme, les côtés étant parallèles deux à deux.

Les moitiés sont égales. Sur chacune des quatre pièces les côtés rouges sont égaux.

Par symétrie, c'est aussi le cas pour les côtés verts. (invariance du carré par rotation de 90°).

2) À partir du positionnement des deux segments rouges et verts, le fait de tracer les parallèles (roses) montre que les deux autres côtés sont égaux. Les huit pièces sont isométriques (superposables).

3) Figure de gauche: le quadrilatère vert en bas est un rectangle car il a quatre angles droits du fait du tracé des parallèles.

4) Figure de droite: les segments rouges, un des côtés des pièces, ont même longueur. Pour chaque pièce: "rouge" diminué de "vert" = côté du petit carré (en haut), que l'on retrouve comme côté du rectangle (en bas). Ses côtés sont égaux, ce rectangle est un carré. Les deux carrés verts sont de la même taille (isométriques).

Dissections (puzzle) à sept et huit pièces		haut
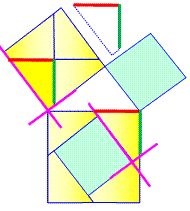
La configuration classique du triangle flanqué de ses trois carrés. aD'autres carrés sont dessinés, dont le vert identique au petit carré qui servira à découper les pièces à la place de l'original. Le puzzle consiste à reconstituer le grand carré oblique avec les pièces provenant des deux carrés plus petits. Les pièces sont nommées de A à G.
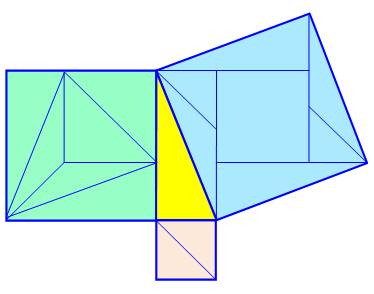
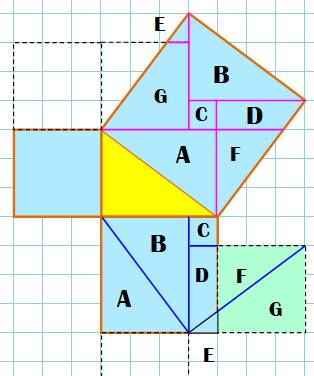
Une autre dissection de la même forme à trois carrés autour du triangle rectangle de base (jaune foncé). Petit carré coupé par sa diagonale et prolongée dans le grand carré. Moyen carré flanqué de deux triangles rectangles jaunes. Le côté extérieur est prolongé dans le grand carré. Grand carré découpé par les prolongement des côtés des petit et moyen carrés et leurs parallèles issues des sommet. Découpe d'un tout petit carré central, reporté dans le moyen carré.
Une autre dissection, datant de 1886, est due à Eduard Böttcher (1847-1919), physicien allemand. Une grande diagonale coupe le petit carré et le carré moyen, chacun en deux. Les côtés du grand carré sont prolongés pour achever la dissection entre quatre pièces dans chacun des deux carrés. Ces pièces sont réassemblées pour reconstituer le grand carré. Intérêt d'une découpe initiale simple, mais d'un réarrangement surprenant.

Haut de page

Retour	Démonstrations du théorème de Pythagore – Similitudes
Suite	Démonstration chinoise (Chou Pei)
Voir	Triangles rectangles Triangles – Index
Sites	Découpage d'Airy et théorème de Pythagore – Serge Cantat Théorème de Pythagore : dissection de Perigal – Cordierphychi – Vidéo Geometric Dissections and Transpositions (1891) by Henry Perigal La secte des nombres – Claudi Alsina – CNRS – Certaines dissections de cette page sont inspirées de celles présentées dans cet article – D'autres solutions y sont proposées Dudeney dissection – Takaya Iwamoto Voir liste des autres liens
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/Pavage.htm