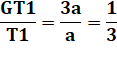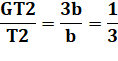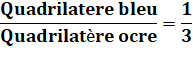|
Édition du: 04/08/2023 |
|
INDEX |
Quadrilatères |
||
|
Quadrilatère
– Introduction |
Quadrilatère
– Aire |
||
|
Dissection
(bi- tri- quadri-) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Dissection du quadrilatère Propriétés
des polygones
construits par dissection du quadrilatère quelconque. |
||
|
|
Sommaire de cette page >>> Dissection en
deux >>> Trisection du
quadrilatère >>> Quadrisection du
quadrilatère >>> 8-section du
quadrilatère |
Débutants Glossaire |
|
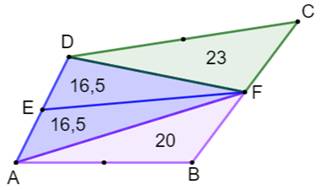
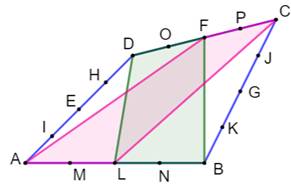
Propriété élémentaire Le segment EF est une des deux bimédianes du
quadrilatère; AF et DF sont les semi-diagonales. Les triangles AFE et DFE ont la même aire. Les triangles BEF et CFE ont la même aire. Même propriété avec la seconde bimédiane. Démonstration Deux
triangles de même sommet et de bases alignées ont des aires dans le
rapport de leur base. Les triangles AFE et DFE ont:
|
|
|
|
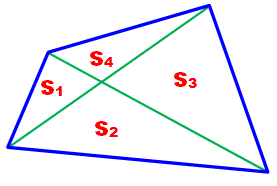
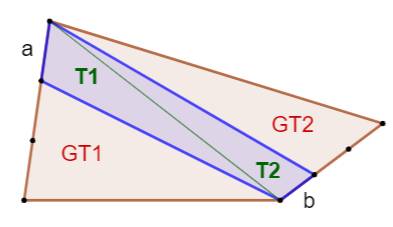
Propriété avec les diagonales
Voir Démonstration |
|
|
|
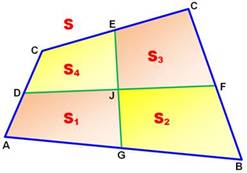
Propriété avec les bimédianes Droites qui relient les milieux des côtés opposés
Voir Démonstration |
|
|
|
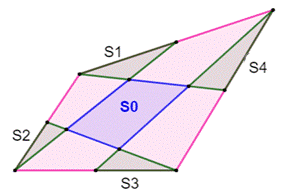
Propriété avec médianes Droites qui joignent un sommet au milieu du côté
opposé
Somme des aires
vertes et bleue = 0,4 S Somme des aires
roses = 0,6 S |
S0 = 1/5 S |
|
|
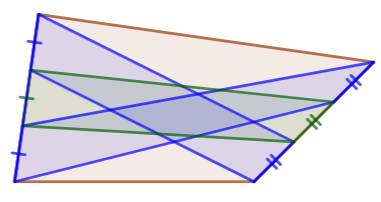
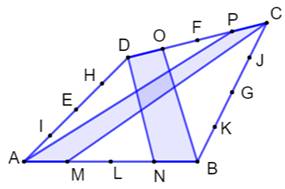
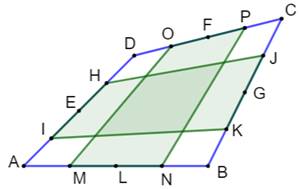
Construction Un quadrilatère convexe quelconque. Les côtés opposés sont partagés en trois segments
égaux. Note: les
segments vers sont les trimédianes Propriété L'aire de chacun des trois quadrilatères (bleus
et vert) est égale à un tiers de celle du quadrilatère complet. |
|
|
|
Démonstration Soit
deux triangles de même sommets et de bases alignés, alors le rapport des
aires est égal au rapport des bases.
La somme:
|
|
|
|
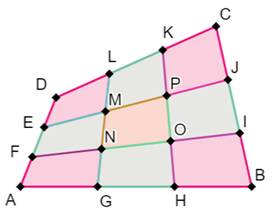
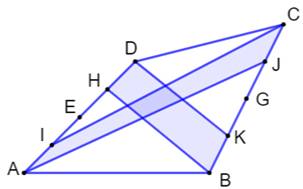
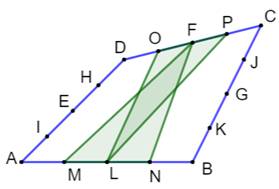
Trisection des quatre côtés Chacun des côtés est partagé en rois segments
égaux. Propriété des longueurs EM = MP = PJ FN = NO = OI GN= NM = ML HO = OP = PK Les quatre trimédianes sont, elles aussi,
partagées en trois parties égales. |
|
|
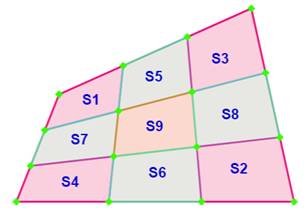
Propriété des aires S1 + S2 = S3 + S4 = S5 + S6 = S7 + S8 = 2 × S9 = 2/9 S (quadrilatère complet) |
S9 = 1/9 S |
|
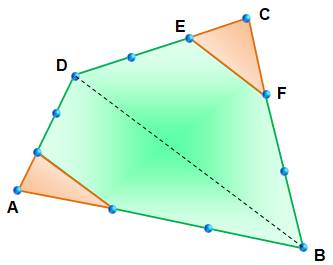
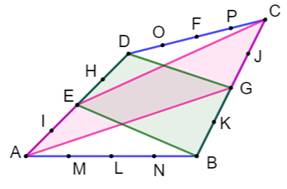
Aire du polygone vert ? SV = 8/9 S Démonstration
(elle est simple) Du fait de la division en trois, EF = 1/3 DB L'aire des triangles CEF et CDB sont dans le même
rapport au carré. Idem pour le triangle ABD. Et, même chose pour leur somme. SV = 8/9 S |
|
|
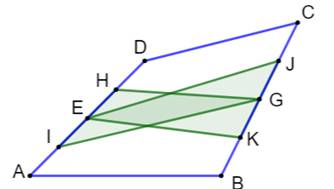
Parallélogramme Les droites passant par les deux points proches
d'un sommet forment un parallélogramme. En effet, chaque côté est parallèle à une des deux
diagonales. |
|
|
Chaque côté est partagé en quatre segments égaux. Ces huit quadrilatères ont la même aire = un quart de celle du
quadrilatère complet |
||
|
|
|
|
|
|
|
|
|
Ces six quadrilatères ont la même aire = la moitié de celle du
quadrilatère complet |
||
|
|
|
|
|
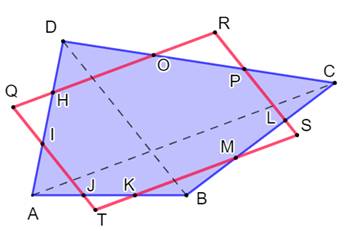
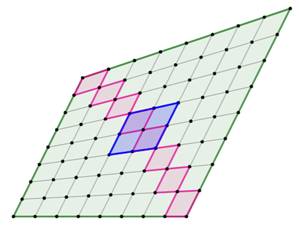
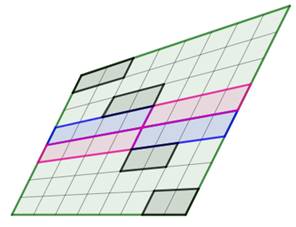
Construction Chacun des côtés du quadrilatère est partagé en
huit parts égales. Propriétés Somme des aires bleues = 1/16 S Somme des aires roses = 1/8 S Même chose sur l'autre diagonale. Figure du bas On retrouve cette proportion également avec les bandes
bleues, roses ou encore grises dans toutes leurs orientations possibles. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |