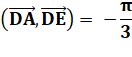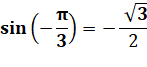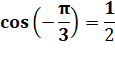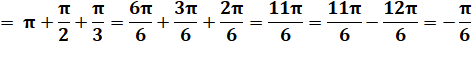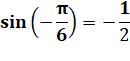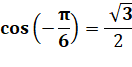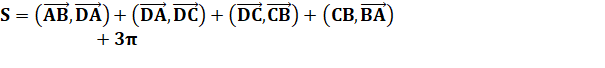NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Base de la Géométrie
Débutants Angles	ANGLES				Glossaire Géométrie
INDEX Angles Bases Géométrie	Première	Angles	Angles orientés	Exemple de calculs
		Sommaire de cette page >>> Angles orientés >>> Propriétés essentielles >>> Exercice avec les angles orientés >>> Triangles >>> Quadrilatères

Les ANGLES orientés

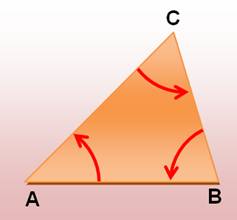
Généralisation de la notion d'angles. Mesure de l'angle entre deux segments de droites quelconques. Comparaison à distance. Idée fort utile pour résoudre systématiquement des problèmes liés aux angles, comme le calcul de la somme des angles dans un polygone.

Les angles sont définis par des vecteurs. Le sens de parcours de l'angle importe. Cette notion va trouver son plein emploi en trigonométrie.

Voir Pourquoi avoir choisi le sens antihoraire comme sens positif en maths

Angles orientés
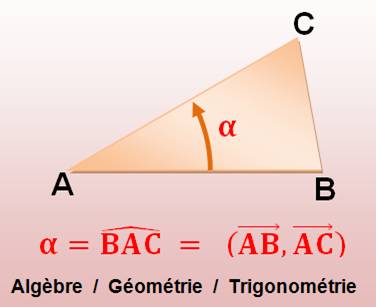
Définition Nous avions l'habitude de nommer un angle par: une lettre (ici alpha) en algèbre; en géométrie, nous avions besoin de bien signaler qu'il s'agit d'un angle; en trigonométrie, nous allions tenir compte de son orientation: positif pour le sens antihoraire, et négatif pour le sens horaire. Évidemment, l'angle n'est défini que si les vecteurs AB ou AC ne sont pas nuls.
Pourquoi? Essentiellement pour une généralisation de la notion d'angle sans avoir besoin du sommet de l'angle. Soit deux vecteurs non nuls: et trois points ABC tels que , on appelle angle orienté le couple de ces deux vecteurs.	Sans ambiguïté, on omet le chapeau. Certains séparent les vecteurs avec un;
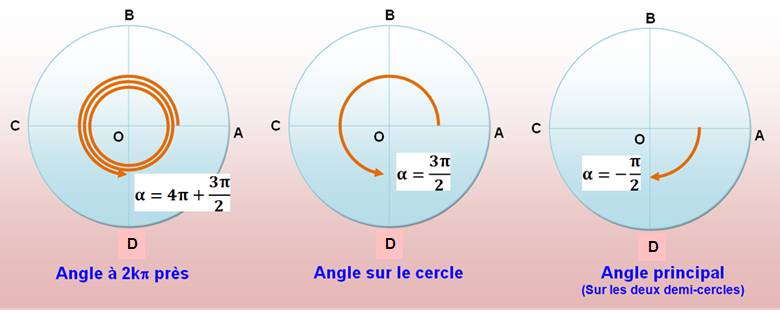
Unités Les angles se mesurent en radians: Ces quelques exemples de conversions montrent comment s'y prendre en utilisant le classique produit en croix. Valeurs Il existe trois types de valeurs pour la mesure d'un angle. Pour tous on dessine un cercle de rayon unité comme guide (cercle trigonométrique). L'angle principal est celui qui précise la valeur entre . Les crochets ] … ] veulent dire qu'en C on donne la valeur Pi et non –Pi.

Propriétés essentielles
Colinéaires Parallèles Orthogonaux Bissectrice	Si l'angle vaut les deux vecteurs sont parallèles. Trois points distincts A, B et C sont alignés si Si l'angle vaut les deux vecteurs sont orthogonaux. Si alors AM est la bissectrice de l'angle .
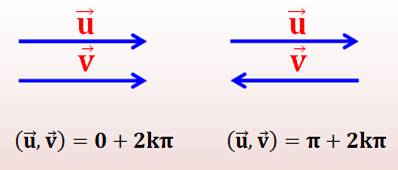
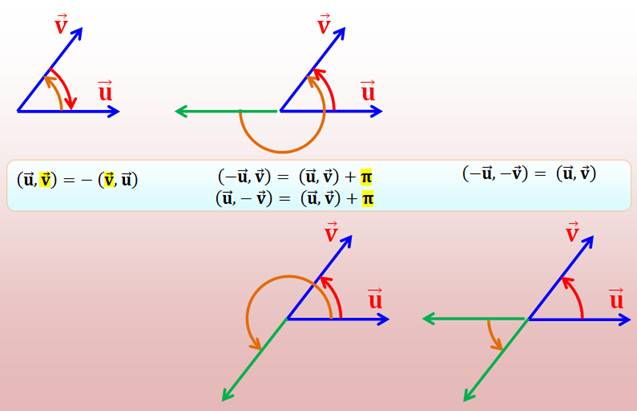
Égalités (toutes ces valeurs sont à 2k Pi près)
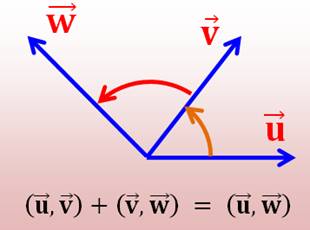
Addition Relation de Chasles

Voir Je débute et je voudrais des explications pas à pas …

Voici d'autres exemples de calculs classiques

Exercice avec les angles orientés
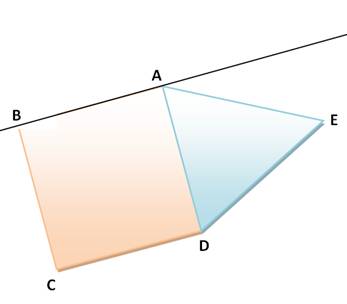
Problème 1 Exprimez l'angle Son sinus et son cosinus. Solution Problème 2 Exprimez l'angle Son sinus et son cosinus. Approche La parallèle à CD en AB montre que notre angle vaut – 30° = – Pi/6.	Figure ABCD est un carré, et ADE est un triangle équilatéral. Dans un triangle équilatéral, les trois angles valent 60° = Pi/3
Calcul avec la relation de Chasles pour les angles On se sert de A comme origine des angles.

Triangles
La relation de Chasles appliquée aux angles orientés est très précieuse. Nous allons démontre que la somme des angles du triangle est égale à 180° sans pratiquement l'aide de la figure. Avec Chasles nous allons essayer de partir de A et revenir à A.	Tous les angles sont donnés à 2k Pi près.
Pour cela nous allons utiliser les égalités vues ci-dessus. En reprenant cela dans notre somme: En mettant dans l'ordre qui nous convient pour constituer une chaine, nous en profitons pour éliminer un tour (2Pi): La relation de Chasles s'applique à cette liste en chaine: Application de la relation sur les vecteurs colinéaires, l'un opposé à l'autre:

Voir Démonstration géométrique

Quadrilatères – Somme des angles
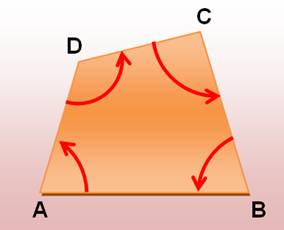
Que vaut la somme S des angles du quadrilatère?
Nous allons utiliser le même procédé que pour le triangle: nous retournons les trois premiers angles orientés: En reprenant cela dans notre somme et en ordonnant, sachant que 3 Pi équivalent à 1 Pi: Bilan, tout en restituant le 2k Pi près que nous avons omis par souci de légèreté:

Voir Démonstration géométrique

Merci à Olivier Duwat pour sa relecture attentive

Suite	Exemple de calculs Trigonométrie
Voir	Anamorphoses Droites Fractales Géométrie – Index Géométrie – Vue d'ensemble Homothétie – Débutant Mathématiques Théorème de Thalès en action Transformation du boulanger Transformations Triangles– Index
Aussi	DicoMot DicoNombre Théorie des nombres – Index Jeux, énigmes – Index Humour et pensées – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Bases/Anglorie.htm