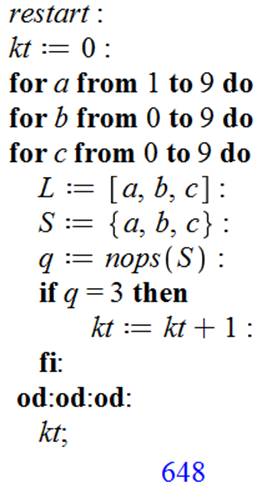|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES avec k chiffres différents Compter
les nombres à n
chiffres formés de k chiffres
différents (exactement ou au moins). Tableau récapitulatif in fine. |
|
|
||
|
Pour commencer un problème classique qui
circule sur les forums. Problème Nombre de
quatre
chiffres, composé
de deux
chiffres au plus. Combien y
en a-t-il? |
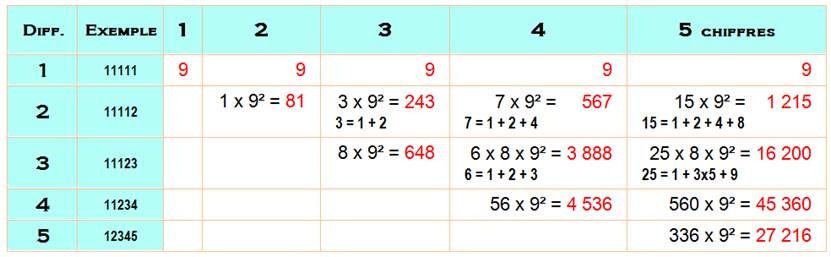
Exemples
|
|
|
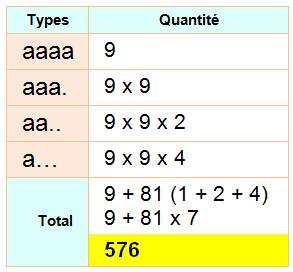
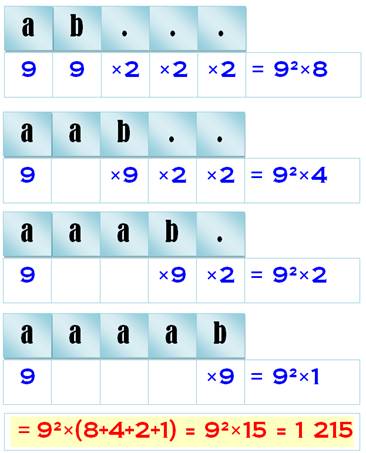
Observations Le
tableau montre des exemples numériques de ce que nous attendons. Quatre
configurations possibles. Voyons cela. Configuration aaab Les
plages en jaune montrent ce qui se passe pour la configuration aaab. Effectivement b peut prendre toutes les valeurs de
0 à 9, sauf la valeur de a. Soit 9 nombres de ce type pour chaque valeur de
a. Or, le chiffre de tête (a), peut prendre les valeurs de 1 à 9, soit 9 cas.
Configuration ab.. Les
plages en rose montrent deux exemples d'une telle configuration. Dans les
deux cas, il existe quatre possibilités pour les deux derniers chiffres. Comptons:
Bilan ab.. => 9 x 9 x
4 possibilités. Configuration aa.. Exemple
avec les plages en bleu. Dans ce cas, on ne compte que deux possibilités pour
les deux derniers. Comptons:
Bilan ab.. => 9 x 9 x
2 possibilités. Configuration aaaa La plus
simple. Bilan aaaa => 9 possibilités. Total
Vérification Le
tableau à droite compte 63 lignes pour chaque chiffre de tête 1 ou 2. Soit 9
x 63 = 567 pour les neuf chiffres. Sans
oublier les 9 nombres à chiffre unique: 567 + 9 = 576. |
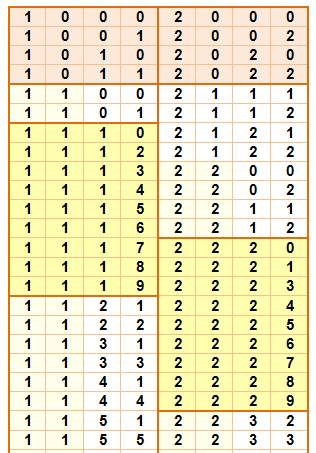
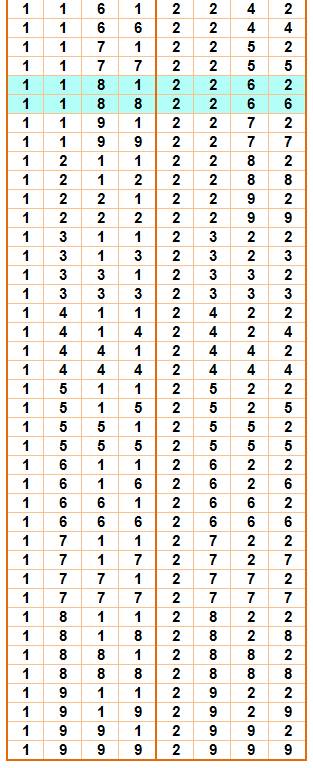
Exemple: tableau avec le premier
chiffre à 1 et à 2
|
|
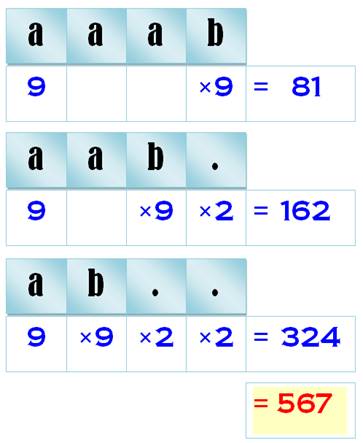
Présentation résumée Nombres à
quatre chiffres formés de
deux types de chiffres exactement. Exemple
de lecture pour aab.
Note: pour retrouver le cas vu ci-dessus, il faudrait ajouter les 9 cas de
nombres à chiffres uniques. |
|
|
|
||
|
Problème Nombre de
quatre chiffres, composé
de trois chiffres exactement. Combien y
en a-t-il? Commentaires Le
dénombrement n'est pas difficile, une fois assimilé le principe exposé
ci-dessus. Par
contre, plus difficile, identifier les toutes les configurations, sans
doublons. Les deux exemples suivants vont aider à
comprendre. |
Résolution
|
|
|
|
||
|
Problème Nombre de
cinq chiffres, composé
de deux chiffres exactement. Combien y
en a-t-il? Commentaires Observez la régularité des comptes: 9² x puissance de
2. |
Résolution
|
|
|
|
||
|
Problème Nombre de
cinq chiffres, composé
de trois chiffres exactement. Combien y
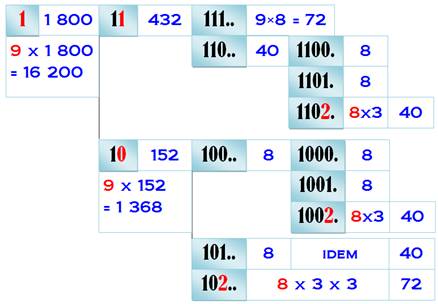
en a-t-il? Commentaires Une méthode plus rassurante consiste à
examiner tous les cas avec le 1 pour en-tête. On
commence par dessiner les blocs de configuration (bleus) jusqu'au bout à
droite, puis on compte en remontant vers la gauche. Les
chiffres en rouge sont ceux qui peuvent prendre toutes les valeurs sauf
celles déjà utilisées. |
Résolution
Nombres
à cinq chiffres dont trois différents exactement: 16 200. |
|
|
Exemple de lecture: il existe:
|
|
|
||
|
|
L'instruction restart (redémarre) efface tout ce qui pourrait rester
des calculs précédents. Initialisation à 0 d'un compteur nommé kt. Mise en route de trois boucles qui vont explorer les paramètres a, b
et c représentant les chiffres du nombre à étudier. L est la liste qui donne par exemple [1, 1, 2]. S est l'ensemble formé
à partir de la liste. Ici: {1, 2}. Cette opération a pour effet de supprimer
les doublons. q est la quantité de nombres dans S; cad. la
quantité de chiffres différents dans le nombre. Si cette quantité est égale à 3, faire croitre le compteur d'une
unité. Fin de la condition (fi) Fin des trois boucles (od:od:od) Imprimer la valeur du compteur. Dans ce cas, 3 chiffres différents dans un nombre à 3 chiffres, la
quantité calculée est 648. |
|
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Denombre/aaaChiff/Chiffdif.htm |
![]()