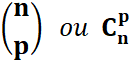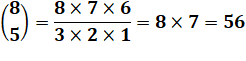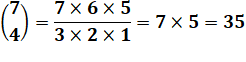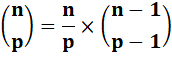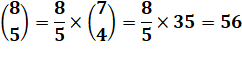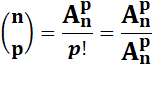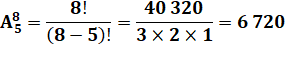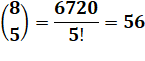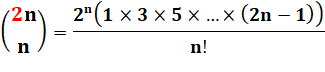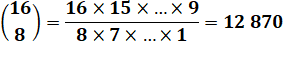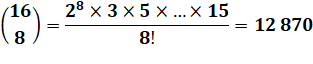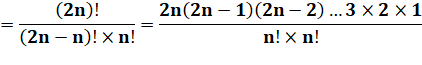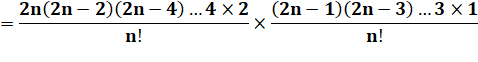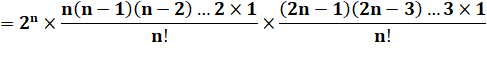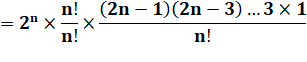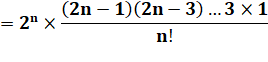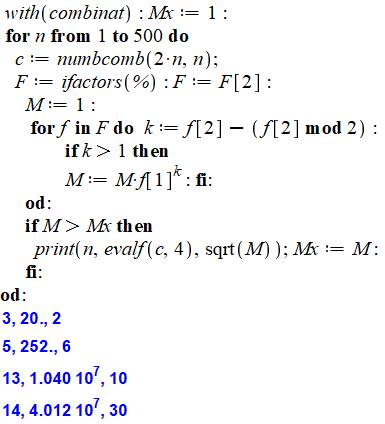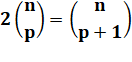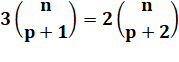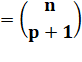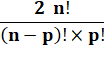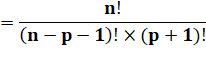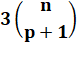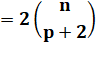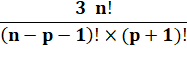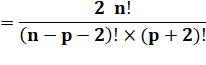NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants COMPTER FAQ	COMBINAISONS			Glossaire COMPTER
INDEX Dénombrement Calculs	Général	Théorie	Simple	Hypergéométrique
	Répétitions	Exemple 4 parmi 8	Somme distinctes	Énumération
		Sommaire de cette page >>> Valeurs et relations >>> Doubler >>> Conjecture d'Erdös >>> Équations

Combinaisons – Calculs

Valeurs et relations
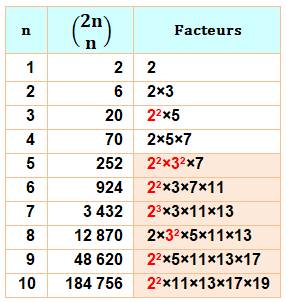
Voir VALEURS en coefficient du binôme	Exemples

Doubler
Formule
Exemple
Démonstration
On sépare pair et impair
On extrait le 2 de tous les facteurs pairs
Mise en évidence de n!
Simplification

Conjecture d'Erdös				haut
Paul Erdös (1913-1996) et sa conjecture concernant la quantité de combinaisons: Conjecture La quantité de combinaisons de 2n objets pris n par n (n > 4) est divisible par un nombre carré. Démontrée par A. Granville et O. Ramaré. Exemple Dix objets pris 5 par 5 conduit à 252 combinaisons possibles, et ce nombre est divisible par 6 au carré.		Table
Propriétés Les combinaisons en 2^k × 8 ne sont pas divisibles par 4, comme 8, 16, 32, 64 … Par exemple, avec n = 64, le nombre (2,39… 10^37) est divisible par 55².	Calcul et simplification avec n = 8 Seul un facteur 2 subsiste !
Table des records de carrés jusqu'à n = 500 Ex: le nombre de combinaisons de 28 parmi 14 est divisible par le carré de 30, et c'est le plus petit nombre avec ce carré supérieur au précédent (10). Aussi, la quantité de combinaisons est égale à: 40 116 600 ≈ 4,012 × 10^7 Programme Maple Voir Programmation – Index

Résolution d'équations
Trouver n et p sachant que
Première équation
Développons en factorielles
Simplification par n! et produit en croix	2 (n – p – 1)! (p+1)!	= (n – p)! p!
En sortant un facteur des factorielles	2 (n – p – 1)! (p+1) p!	= (n –p) (n – p – 1)! p!
Simplification	2 (p+1) 2p + 2 3p – n + 2	= (n – p) = n – p = 0
Deuxième équation
Développons en factorielles
Simplification par n!	3 (n – p – 2)! (p+2)!	= 2 (n – p – 1)! (p+1)!
En sortant un facteur des factorielles	3 (n–p-2)! (p+2)(p+1)!	= 2 (n–p–1)(n–p–2 )! (p+1)!
Simplification	3 (p+2) 3p + 6 5p – 2n + 8	= 2 (n – p – 1) = 2n – 2p – 2 = 0
Système d'équations	3p – n + 2 5p – 2n + 8	= 0 = 0
Deux fois la 1^ère moins la 2^e	p – 4 p	= 0 = 4
En remplaçant dans la 1^ère	12 – n + 2 n	= 0 = 14

Suite	Combinaisons – Cas simples Rang d'une combinaison
Retour	Combinatoire – Index D'un coup d'œil
Voir	Cartes Compter les nombres Dés Dominos Échecs Factorielle et ses cousines Grenouilles Jeux – Index Probabilités Triangle de Pascal
Cette page	http://villemin.gerard.free.fr/Denombre/Cbintheo.htm