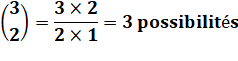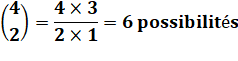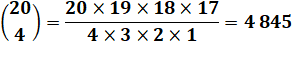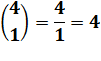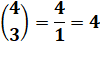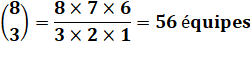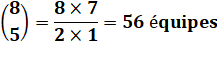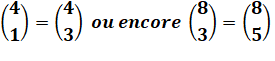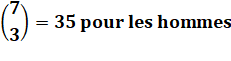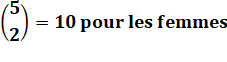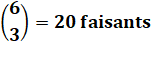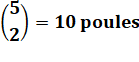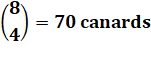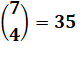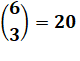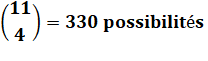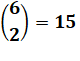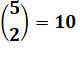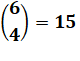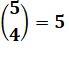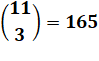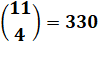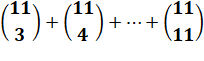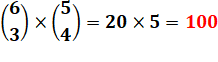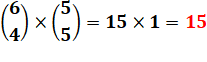|
||||||||||||||||||||||||||||
![]()
|
COMBINAISONS Étude de cas simples Rappels Voir calcul en pratique |
Expression anglaise:
the three men can be chosen from the seven men in 35 ways
|
|
||||
|
Ensemble |
Choix |
Calcul |
||
|
Test comportant 3
problèmes |
Examen:
en résoudre 2. |
|
||
|
Test comportant 4
problèmes |
Examen:
en résoudre 2. |
|
||
|
20 contribuables |
L'inspecteur
peut en voir 4 dans la journée. |
possibilités
d'organiser sa journée |
||
|
4 lettres {a, b, c, d} |
sélections
de 1 lettre |
Effectivement: a ou b ou c ou d |
||
|
idem |
sélections
de 3 lettres |
Soit: abc,
abd, acd, bcd |
||
|
8 personnes |
équipes
de 3 |
|
||
|
idem |
équipes
de 5 |
|
||
Remarques
|
Les
coefficients à égale distance des extrémités sont égaux (somme en bas égale
valeur en haut)
Il
est plus facile de calculer avec celui qui donne le moins de facteurs (le
plus petit nombre en bas). |
Voir Calcul des
coefficients du binôme en pratique
|
|
|||
|
Ensemble |
Choix |
Calcul |
|
|
Groupe
de 7
hommes 5
femmes |
Comité
formé de 3
hommes 2
femmes |
Choix indépendants Total = 35 x 10 = 350 possibilités de comités |
|
|
Marché 6
faisans 5
poules 8
canards |
Achats 3
faisans 2
poules 4
canards |
Choix indépendants Total = 20 x 10 x 70 = 14 000 possibilités d'achat |
|
|
Examen
en 2 parties A et B de
7 questions et
6 questions |
Répondre
à
4 questions de A et
à 3 questions de B |
Choix indépendants Total = 35 x 20 = 700 possibilités de réponses |
|
|
|
|||
|
Ensemble |
Choix |
Calcul |
|
|
Sac
de 11 billes 6
blanches 5
rouges |
4
billes quelconques |
|
|
|
On
veut 2
blanches et 2
rouges |
Choix indépendants Total = 35 x 20 =
700 possibilités
de réponses |
||
|
On
les veut les 4 de la même couleur |
Ce sont deux
cas de choix différents Total = 15 + 5 =
20 possibilités |
||
|
Groupe
de 12
personnes |
Comité
de 5
personnes dont
un Président |
Choix du Président A = 12 possibilités Formation du comité parmi les personnes restantes
Choix indépendants Total = 12 x 330 =
3 960 possibilités |
|
|
|
|||||||||||||||||||||||||||||
|
Ensemble |
Choix |
Calcul |
|||||||||||||||||||||||||||
|
11
amis |
Invitation
de 3 amis à votre cocktail |
|
|||||||||||||||||||||||||||
|
Invitation
de 4 amis à votre cocktail |
|
||||||||||||||||||||||||||||
|
… |
|
||||||||||||||||||||||||||||
|
Invitation
de 3 amis ou plus
à votre cocktail |
=
165 + 330 + … voir
tableau ci-dessous =
1 981 possibilités
d'invitations |
||||||||||||||||||||||||||||
Voir Tableau complet |
|||||||||||||||||||||||||||||
|
Madame
a 11
amis: 5
hommes et 6
femmes |
Invitation
de 3 amis à votre cocktail avec autant
d'hommes que de femmes |
Avec Madame,
cela fera 4 personnes: 2 hommes et 2 femmes. Étant
elle-même femme, elle doit choisir une autre femme: Ensuite, elle
choisit deux hommes: Soit : 6 x 10 = 60 types
d'invitations |
|||||||||||||||||||||||||||
|
Invitation
de 4 à votre cocktail avec autant d'hommes que de femmes |
4 invités plus
madame: pas possible d'avoir autant d'hommes que de femmes |
||||||||||||||||||||||||||||
|
Invitation
de 5 à votre cocktail avec autant d'hommes que
de femmes |
Étant
elle-même femme elle doit choisir deux autres femmes: Ensuite, elle
choisit trois hommes: Soit : 15 x 10 = 150
types d'invitations |
||||||||||||||||||||||||||||
|
Pour
7 |
|
||||||||||||||||||||||||||||
|
Pour
9 |
|
||||||||||||||||||||||||||||
|
Invitation
de 3 amis ou plus
à votre cocktail avec autant d'hommes que de femmes |
60 + 150 + 100 + 15 = 325 types d'invitations. |
||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()