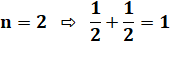NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/08/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Général	Selon leurs diviseurs				Glossaire Général
INDEX Types de nombres	Parfaits	Semi-parfaits (SP)	SP Primitifs	SP Primaire
	Refactorisables	Pratiques	Abondant primitifs	Friables
	Facteurs-Diviseurs	Intouchables	Chiffres distincts	Giuga
	Consommables	Glissants ou SBF
		Sommaire de cette page >>> Nombres SP primaires >>> Liste des SP primaires connus >>> Programmation >>> Nombres multi-parfaits

Famille	Nombre / Division / Diviseurs
Approche	Un nombre: 10 Ses facteurs: 10 = 2 x 5 La somme des inverses: 1/2 + 1/5 + 1/10 = 4/5 = 0,8. Est-il possible que cette somme d'inverse soit égale à 1 ? Oui, mais c'est rare ! Résultats pour les nombres de 1 à 10 Les nombre 2 et 6 sont semi-parfaits primaires

Définitions	Nombre semi-parfait primaire ou nombre pseudo-parfait primaire: Nombre entier n, produit de facteurs distinct et tel que:
Exemples
Exemple de calcul

Voir Introduction et place des semi-parfaits

Propriétés

La définition peut être relâchée avec les mêmes nombres en résultats parmi tous les nombres et l'ensemble des facteurs: chaque facteur est compté une fois même s'il a un exposant. la condition la somme 1 peut être étendue à n'importe quel entier, sans changer les nombres produits.

Les huit semi-parfaits primaires connus
2 6 42 1 806	= 2 = 2 x 3 = 2 x 3 x 7 = 2 x 3 x 7 x 43
47 058	= 2 x 3 x 11 x 23 x 21
2 214 502 422	= 2 x 3 x 11 x 23 x 31 x 47059
52 495 396 602	= 2 x 3 x 11 x 17 x 101 x 149 x 3109
8 490 421 583 559 688 410 706 771 261 086 = 8, 4 … 10^30	= 2 x 3 x 11 x 23 x 31 x 47059 x 2217342227 x 1729101023519

Programmation
	Commentaires Ouverture du logiciel de théorie des nombres. Boucle d'analyse des nombres n de 1 à 10 000. Demande du jeu de facteurs du nombre n (factorset) et la quantité de facteur en q. Calcul de la somme (add) de l'inverse du nombre n et des inverses des facteurs (F[i]). Si la somme est égale à 1, le nombre est semi-parfait primaire, alors imprimer n et F. Fin de boucle (od). Résultats en bleu après quelques secondes de calculs.

Voir Programmation – Index

Nombres multi-parfaits

En prenant les diviseurs et non les facteurs, selon le même principe de sommation des inverses, on retrouve les nombres parfaits et multi-parfaits.

Exemple avec la quadri-parfait: 30 240

la somme de ses diviseurs est égale à quatre fois 30 240.

la somme de l'inverse de ses diviseurs est égale à 4.

30 240: diviseurs {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 54, 56, 60, 63, 70, 72, 80, 84, 90, 96, 105, 108, 112, 120, 126, 135, 140, 144, 160, 168, 180, 189, 210, 216, 224, 240, 252, 270, 280, 288, 315, 336, 360, 378, 420, 432, 480, 504, 540, 560, 630, 672, 720, 756, 840, 864, 945, 1008, 1080, 1120, 1260, 1440, 1512, 1680, 1890, 2016, 2160, 2520, 3024, 3360, 3780, 4320, 5040, 6048, 7560, 10080, 15120, 30240}.

Voir	Nombres refactorisables Diviseurs Factorielles Dénombrement – Combinatoire Compter les sous-ensembles Fractions égyptiennes Somme de fractions = 1
DicoNombre	Nombre 42 Nombre 1 806 Nombre 8, 4 … 10^30
Sites	Primary pseudoperfect number – Wikipedia OEIS A 054377 – Primary pseudoperfect numbers: numbers n > 1 such that 1/n + sum 1/p = 1, where the sum is over the primes p | n.
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Primaire.htm