|
Édition du: 05/03/2024 |
Faites un double-clic pour un retour en haut de page
![]()
|
TOURNOIS & GRAPHES Définition et propriétés des graphes représentant des tournois. Rappel: un graphe est tout simplement un ensemble de points
reliés par des traits. Les points sont les sommets
et les traits, les arêtes. Si toutes les
arêtes sont présentes, le graphe est complet.
Si les arêtes sont des flèches, le graphe est orienté. Dans un tournoi, le graphe est orienté et complet. |
||
|
|
Sommaire de cette page >>> Tournois comme
graphes >>> Tournois
réductibles et irréductibles >>> Tournois
fortement connexes >>> English corner |
Débutants Glossaire |
Anglais :
Tournament, a n-tournament
|
Définition Un n-tournoi est un ensemble de n points étiquetés, dont chaque paire A, B est reliée soit par
la ligne orientée AB, soit par la ligne orientée BA. C'est un graphe
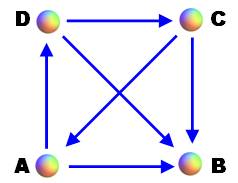
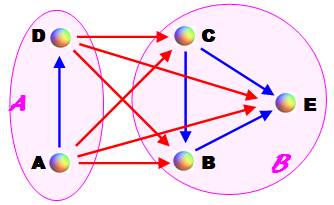
complet: chaque sommet est relié à tous les autres. Il est orienté: chaque arête est dirigée d'un sommet vers l'autre. Chaque paire de sommet est relié par une arête et une seule. Tournoi Dans la représentation des tournois,
les sommets sont les participants. L'arête représente une partie du tournoi.
L'orientation indique le gagnant. Par exemple, sur la figure, C bat A; on dit
que C domine A. |
Exemple de tournoi à quatre
|
||
|
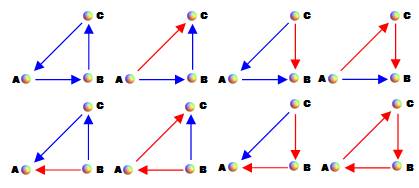
Propriété Un tournoi à n participants possède Q = ½ n (n – 1) paires orientées. En langage de graphe on dira: un graphe représentant un tournoi à n participants
comprend Q arêtes. Selon le choix de l'orientation des arêtes, il existe 2n
graphes possibles. Pour un tournoi à trois participants, il y a 23
= 8 possibilités (Illustration). |
Les huit graphes
pour un 3-tournoi
|
||
|
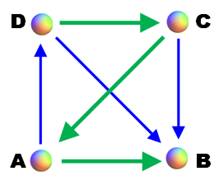
Chemins passant par tous les
sommets Un tel chemin orienté est dit hamiltonien:
il passe par tous les sommets, et cela une seule fois. Théorème de Laszlo Redei (1934) Tout tournoi à n participants (n fini) contient
au moins un chemin (orienté) hamiltonien. |
Exemple de chemin hamiltonien
(vert)
|
||
Exemples de représentation de tournois
à cinq et six sommets
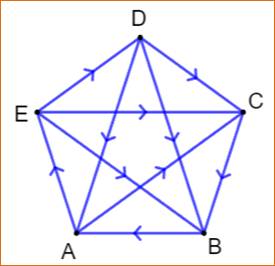
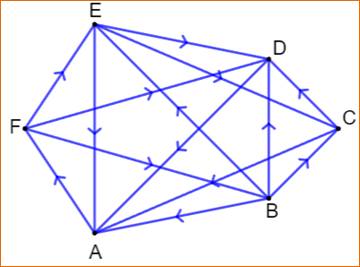
|
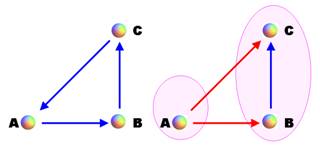
Définition Un tournoi est réductible si: 1.
les
sommets peuvent être séparés en deux sous-ensembles non vides A et B; 2.
chaque
arête joignant un point dans A à un point dans B est dirigée vers un point de B. Dans le cas contraire, le tournoi est irréductible. Cas des huit 3-tournois (voir
figure complète ) Ils sont tous réductibles, sauf le premier (ici,
à gauche) |
Exemple de tournoi réductible à
deux ensembles
Toutes les arêtes sortant de A pointent de A vers
B. |
|
|
Définition Un sous-graphe d'un graphe orienté est fortement connexe si chaque
sommet est atteignable à partir de chacun des autres sommets du sous-graphe. Un graphe orienté est fortement connexe s'il existe un chemin dans
chaque direction entre toute paire de sommets du graphe. Les cinq maisons raccordées Il s'agit d'un problème combinatoire dont la solution est la quantité
de tournois fortement connexes >>> |
Quantité de tournois
fortement connexes de n sommets. Exemple pour 5 sommets la quantité est 544. 1, 0, 2, 24, 544, 22320, 1677488, 236522496, 64026088576,
33832910196480, 35262092417856512, 72926863133112198144, … |
|
Anglais: Strongly connected component
|
An n-tournament
is a set of n labeled points, each pair A, B of which is joined either by the
oriented line AB or by the oriented line BA. There are
N = n(n –1)/2 such pairs and so Fn different n-tournaments, where
Fn = 2N. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Tournoi.htm
|
|