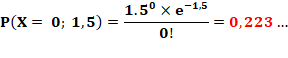NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/08/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Probabilités
Débutants Dénombrement	Lois de probabilités			Glossaire Probabilités
INDEX Combinatoire Probabilités	Introduction	Loi de Poisson	Table Poisson
	Loi des grands nombres	Loi de Bernoulli	Loi Binomiale
		Sommaire de cette page >>> Historique >>> Loi de Poisson >>> Exemple >>> Évolution selon lambda >>> Exemple de calcul – Accidents >>> Exemple de calcul – Erreurs de frappe >>> Applications >>> Propriétés >>> Anglais

LOI de POISSON

Loi qui caractérise les événements rares, comme une série de faits improbables, ou une supposée loi des séries. Par exemple, une suite de crashes d'avions ou de catastrophes ferroviaires (quatre en juillet 2013).

La loi de Poisson décrit la probabilité qu'un événement se produise durant un intervalle de temps donné, alors

que la probabilité de réalisation d'un événement est très faible, et

que le nombre d'essais est très grand.

Voir différences entre: Loi, Distribution, Processus

Historique

Siméon Denis Poisson (1781-1840) abandonne ses études de médecine et devient mathématicien à Paris avec contributions en électricité, magnétisme, orbite des planètes et statistiques.

En 1837, il publie Recherches sur la probabilité des jugements en matière criminelle et en matière civile (texte complet accessible sur Internet). Il y aborde la théorie des probabilités et propose ce qui est désormais appelé la Loi de Poisson.

Les mêmes résultats furent obtenus en 1711 par Abraham de Moivre, lequel aura dû avoir la paternité de cette loi.

Dans ce traité, Poisson propose une formule qui dénombre la quantité d'occurrences que prend une variable aléatoire en un laps de temps. Par exemple, la quantité d'accidents probables en k jours connaissant la moyenne sur un an. En l'occurrence, dans ce traité, elle est appliquée aux délibérations de jurys et, elle passe inaperçue.

En 1898, Ladislaus Bortkiewicz redécouvre cette loi (il l'appelait la loi des petits nombres) pour calculer la quantité de soldats de l'armée prussienne morts accidentellement suite à des coups de pied de cheval. Rutheford, Gosset et Chebyshew (1821-1894) ont également travaillé cette idée. Depuis, la loi de Poisson est devenue un outil de l'ingénierie de la fiabilité.

Poisson a bien obtenu sa formule en analysant des cas concrets. Il se trouve qu'elle est obtenue aussi comme limite de la loi binomiale B(n:p) avec np constant, et aussi de la loi hypergéométrique.

Dans ce traité, Poisson introduit la loi des grands nombres:

Processus et loi de Poisson

On s'intéresse à un grand nombre d'événements indépendants. Événements qui surviennent au hasard. On observe qu'ils se produisent fois en moyenne durant un intervalle de temps donné. La loi de Poisson indique la probabilité que l'événement se produise seulement k fois exactement durant cette période. Illustration du processus de Poisson Formulation avec la variable aléatoire (X). X prend la valeur positive k, entier naturel, avec la probabilité: La probabilité qu'un événement se produire k fois exactement dans une période de temps sachant qu'il s'est déjà produit lambda fois en moyenne est égal à lambda à la puissance k multiplié par exponentielle de moins lambda, divisé par la factorielle de k.

Exemple
Sur ce trajet ferroviaire, nous avons constaté deux incidents par an. Quelle est la probabilité qu'il y en ait exactement dix en dix ans? Quelle est la probabilité qu'il y en ait dix ou moins en dix ans?
La quantité moyenne en dix ans (notre période de temps) se note lambda.	2 par an, soit 2 x 10 = 20 en 10 ans = 2 x 10 = 20
Pour 10 incidents, le calcul (sophistiqué!) de Poisson donne:
Expression que l'on calcule sur une calculette.	P(10; 20) = 0,0058 = 0,58%
Détail du calcul	20^10 = 10 240 000 000 000 e^-20 = 2,061153622 10^-9 10! = 3 628 800
Pour 0 à 10 incidents, le calcul est à exécuter pour toutes les valeurs de 0 à 10. La probabilité cherchée étant la somme. Ici: 1%. Hélas, la probabilité d'avoir plus de 10 incidents en 10 ans est de 99%.	P(de 0 à 10, 20) = P(0; 20) + P(1; 20) + … + P(10; 20) = = 1%
La courbe de la loi de Poisson en fonction de x pour x de 0 à 40. La probabilité de 10 incidents ou moins est représentée par la surface en jaune au pied de la courbe.	Courbe de la loi de Poisson pour = 20

Évolution selon lambda
La courbe est presque symétrique pour les grandes valeurs de lambda qui représente la fréquence de l'événement. Elle est asymétrique et se concentre vers les faibles valeurs pour lambda petit.

Exemple de calcul – Accidents
On a constaté 0,6 accident par jour en moyenne sur 720 jours. Calcul (exemple sur 2 jours) Avec la calculette (ou, ici, avec Maple) Calcul de la fréquence 0,0987 x 720 = 71,126	Le tableau montre, qu'en moyenne, il y aura 395 jours sur 720 sans accident ou encore 632 où on ne déplorera qu'un seul accident au maximum.

Exemple de calcul – Erreurs de frappe
On a constaté 1,5 erreur de frappe par page. Probabilité de 0 erreur: 22,3% Probabilité de plus de 2 erreurs: 19,1% Note: On suppose que les erreurs sont aléatoires et indépendantes.	Calculs

Applications

Gestion des stocks En demande normale, le stock est approvisionné en fonction de la consommation moyenne; Cependant, pour parer aux aléas d'une demande importante soudaine, d'une demande fluctuante ou d'une demande peu fréquente, généralement un stock de sécurité est constitué. La taille du stock est calculée en utilisant la loi de Poisson. Contrôles de qualité Défauts de crédit Accidents, catastrophes Arrivée dans une file d'attente Appels téléphoniques Présence ou absentéisme Plus précisément et par exemple: Quantité de voitures en un point d'un tronçon routier par jour Quantité de fautes de frappe par page dans un texte Quantité d'appels à la minute à un centre d'appels Quantité d'accès par minute à un serveur informatique Quantité de mutation ADN après irradiation Etc.

Propriétés

Paramètres de la loi de Poisson La loi de Poisson s'applique à des variables aléatoires X prenant des valeurs discrètes k (et non continues): P (X = k, ) Lambda est à la fois la moyenne et la variance. Propriété additive de la loi de Poisson Deux variables aléatoires discrètes et indépendantes X et Y. Deux lois de Poisson de paramètre et . Alors la variable aléatoire (X+Y) suit une loi de Poison de paramètre . Valable pour un nombre quelconque de variables. La réciproque est valable. Condition d'emploi de la loi de poisson Un événement se produit durant un intervalle de temps donné avec une probabilité de réalisation très faible, et sur un grand nombre d'occurrences. La loi de probabilité doit être la même durant chacun des périodes de temps (accroissements stationnaires). La loi de probabilité s'applique à des événements indépendants (accroissement indépendants). Cette distribution de Poisson peut être entendue comme la limite de la loi binomiale pour un effectif n tendant vers l'infini et une probabilité d'occurrence p tendant vers zéro. Le produit n.p tend alors vers lambda.

The Poisson distribution (English corner)
Suppose that we can expect some independent event to occur a specified time interval. The probability of exactly k occurrences is equal to P(k; ). It's a function of k (prononcze 'ké') and lambda and the formula says that we take lambda raised to the power k, multiply that by e (prononcez 'i') raised to the negative lambda and divide that by k factorial.
The Poisson distribution describes the probability that a random event will occur in a time or space interval under the conditions that the probability of the event occurring is very small, but the number of trials is very large so that the event actually occurs a few times.

NB. Actually veut dire; en réalité, en fait. >>>

Suite	Table des valeurs de la loi de Poisson
Retour	Probabilité Combinatoire – Rubriques
Voir	Dés Grenouilles Jeux de hasard Probabilités Siméon Denis Poisson – Biographie Trois pièces
Sites	Loi de Poisson – Wikipédia Loi de Poisson – Math93.com – Une Histoire des mathématiques Statistiques par JY Baudot Principales distributions de probabilités – Cours chapitre 3 Gestion des stocks par JY Baudot The Poisson distribution – Université du Massachussetts The Poisson distribution – Science Direct The Poisson distribution – Très nombreux exemples de calcul
Cette page	http://villemin.gerard.free.fr/aMaths/Probabil/Poisson.htm