|
|||||||||||||||||||||||||||||||||||
![]()
|
LOI de POISSON – TABLES Exemple de lecture des tableaux: dans une suite d'événements
indépendants qui se produisent 10 fois en un an en moyenne :
|
|
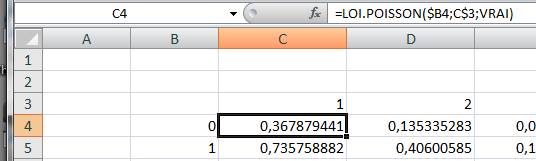
Le tableur Excel offre la possibilité d'un calcul
direct de la loi de Poisson. Voici l'instruction adéquate avec k en premier
puis lambda et enfin vrai pour demander le cumul ou faux pour disposer de la
valeur de la loi de Poisson.
Souvenez-vous
que pour désigner les valeurs absolues d'une cellule (symbole $), il faut
appuyer sur la touche F4 autant de fois que nécessaire. |
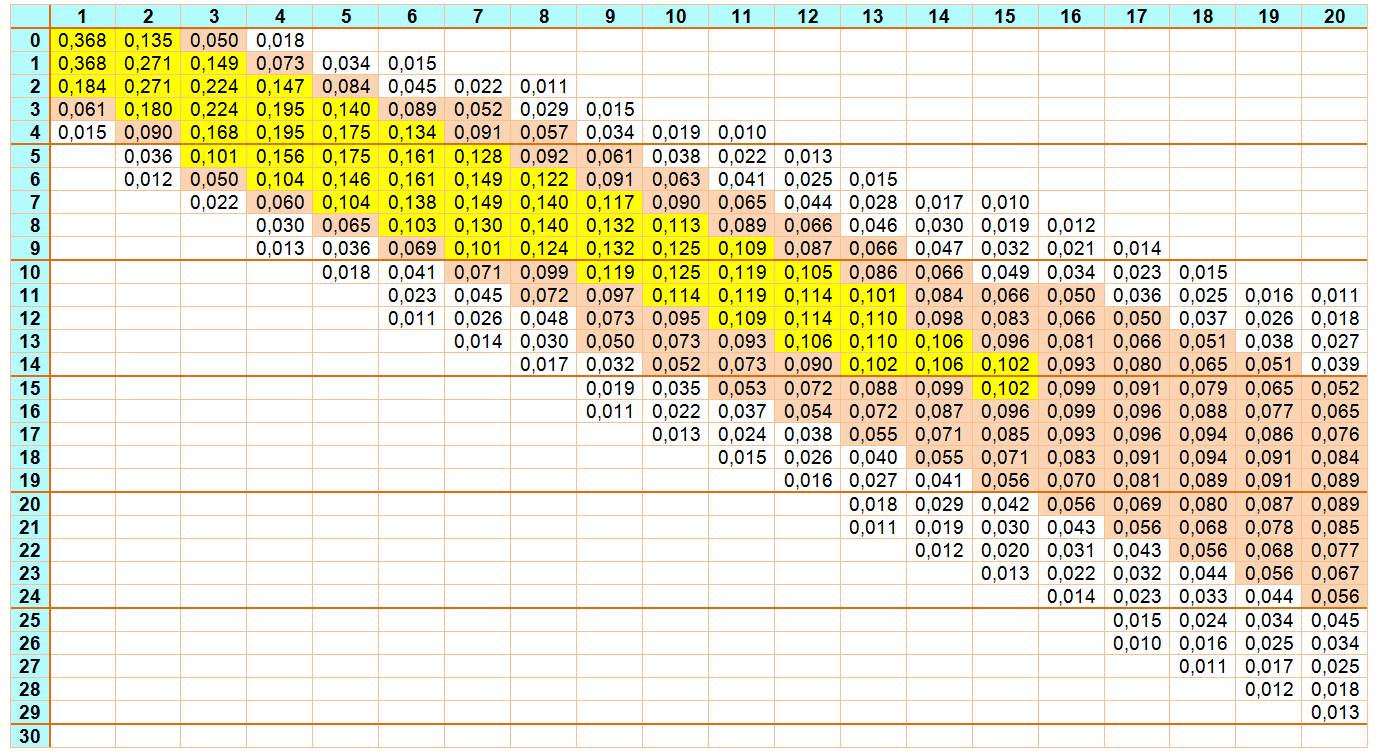
En
jaune valeurs > 0,1; en marron > 0, 05; en blanc >0,01.
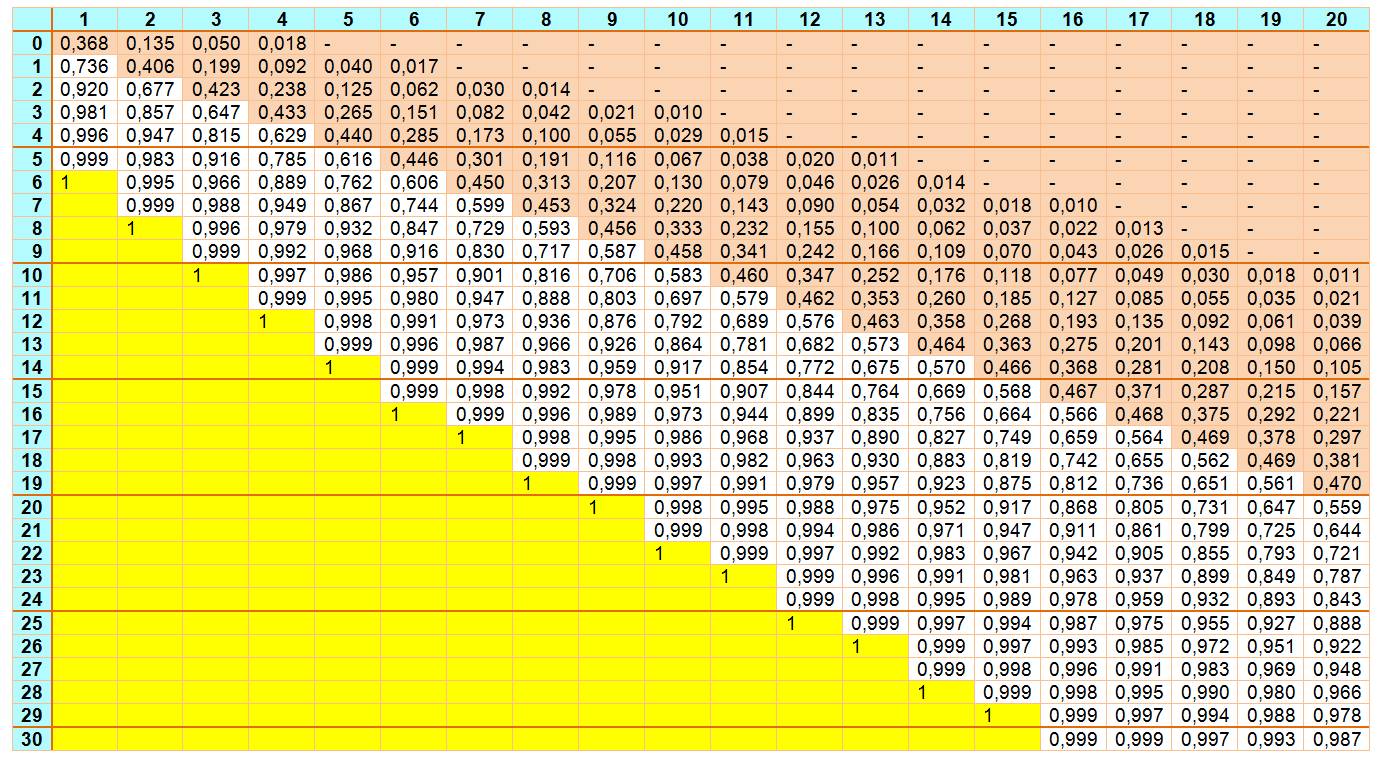
En
jaune valeurs égales à 1 (100%); en marron < 0,5.
|
|
||
|
Quelle est la probabilité de
renvois dans le service qui en traite 100? |
P(k = 0; 2) = 0,135 = 13,5% |
|
|
Une machine-outil en traite
1000 par jour; quelle est la probabilité d'en refuser 2 au plus? |
P(k |
|
|
Quelle est la probabilité
d'y retrouver plus de 5 personnes dans les 10 minutes. |
P(k P(k = 0,384 = 38,4% |
|
![]()
|
Retour |
|
|
Voir |
|
![]()