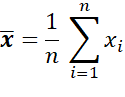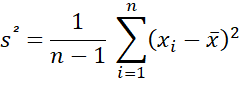|
||||||||||||||||||||||||||||||||||||||||
![]()
|
La
majorité des gens sont plus cons que la moyenne. Cela fait rire pourtant cela peut se
produire. Imaginons que 10 personnes soient cotées 1 sur une échelle d'intelligence
et qu'un individu atteigne les 12. Le total vaut 10x1 + 12 = 22 et la moyenne
22/11 = 2. Dans ce cas, tous sauf un sont plus cons que la moyenne. Ne
pas confondre moyenne et médiane. Note: on
peut aussi écrire "la majorité des gens est plus con que la moyenne". Forme orthographiquement aussi
correcte. Cependant l'intention est de montrer que ce sont les gens qui sont
cons. Alors, on préférera la forme au pluriel. C'est
un type, la tête dans un four et les pieds dans un congélateur? Sa température
moyenne est de 37°C. Le problème, c'est
qu'il est mort! Dites-moi,
en moyenne, on vous donne combien de
pourboire ? – Dix euros, répond l'employé. – Tenez voilà dix euros. – Oh
merci, monsieur, vos êtes le premier à atteindre la moyenne. |
Voir Pensées & humour / Orthographe avec "majorité
de" / Médianes
en géométrie
|
MOYENNES ET MÉDIANES Comment caractériser une
collection de nombres qui semble provenir du hasard ?
Notion de MOYENNE & d'écart
Notion de MÉDIANE & de dispersion |
Voir Médiane
en géométrie
|
|
||||||||
|
|
||||||||
|
|
|
|
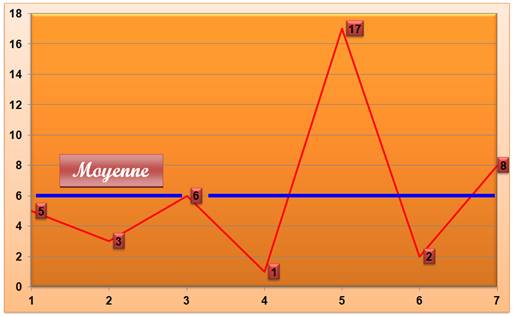
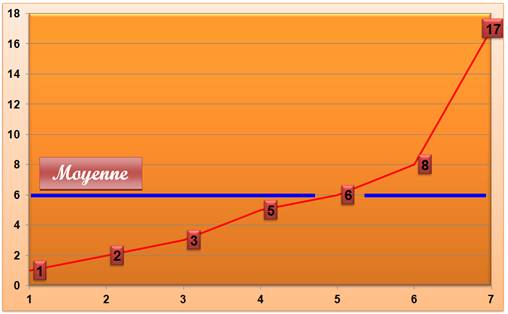
La barre moyenne est telle que: il y a autant au dessus
de la barre que en dessous. Chacun des grands donne un peu au petits pour
qu'au final tous soient de la même taille. Par rapport à la barre de la moyenne, les surfaces
jusqu'à la courbe en dessous et au-dessus sont égales.
Moyenne = Somme des
données / Quantités de données. M = S / n
On
lit:
la
moyenne des x est égal à 1 sur n fois la somme des valeurs de x allant de la
première à la énième. |
|
Voir Symboles
|
|
|
|
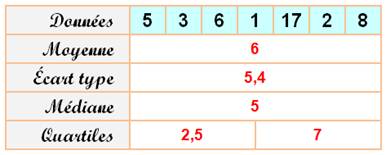
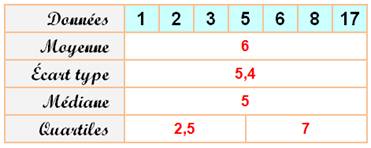
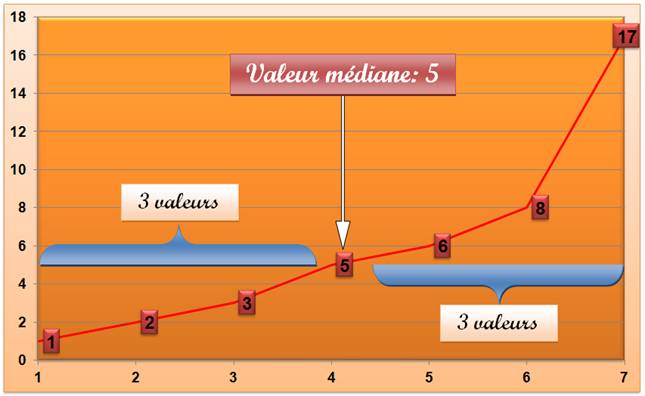
Une fois les données ordonnées, la médiane se révèle
immédiatement. Ici la médiane vaut 5 alors que la moyenne est égale à 6. Lorsque la quantité de valeurs est paire, la médiane
est la moyenne des deux valeurs du milieu. Avec {2, 4,
6, 8}, la médiane serait (4 + 6) / 2 = 5.
|
|
Voir Quartiles,
centiles, quantiles
|
|
|
|
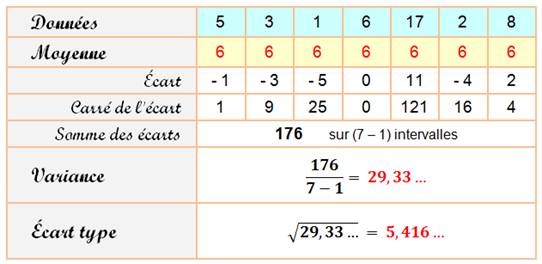
5e ligne, lire: somme
des carrés des écarts
|
|

|
|
||
|
La courbe se décale simplement sur les abscisses,
d'autant plus que la moyenne augmente. |
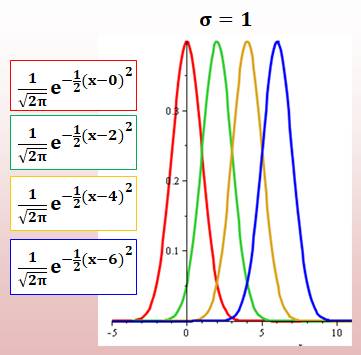
L'écart type varie de 1 à 4.
Un grand écart type (comme
pour la courbe bleue) signifie une grande dispersion des données autour
de la moyenne. |
|
Voir Courbe
gaussienne
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()