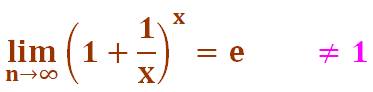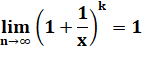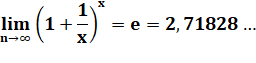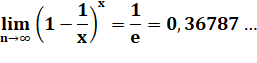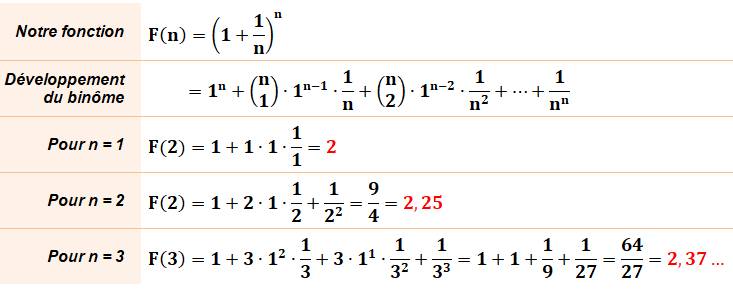|
Édition du: 30/01/2022 |
|
INDEX |
LIMITES |
|||
Faites un double-clic pour un retour en haut de page
![]()
Cette fonction
est plus préoccupante qu'il n'y parait ! Sa limite quand
x tend vers l'infini est e =
2,718281828… Ah !? Pourquoi par simplement 1 ? Voyons comment apprivoiser
cette fonction progressivement. |
|||||
|
Et plus |
Sommaire de cette page >>> Allure des graphes >>> Calcul des valeurs >>> Calcul formel de la limite |
Débutants Glossaire |
|||
|
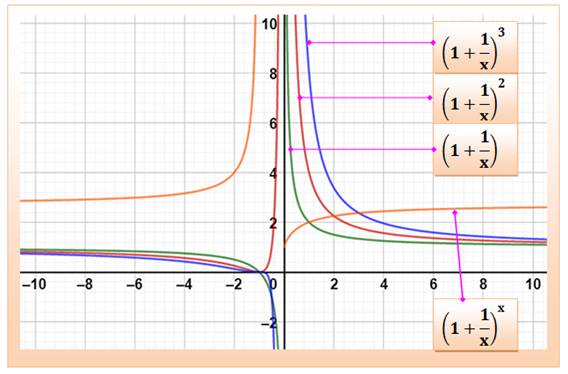
Observation Prenons cette
fonction de base (1+1/x) et portant là à diverses puissances (1, 2, 3 et même
x) et voyons les graphes correspondants. |
Puissance constante Les courbes de la fonction à une puissance constante
sont des hyperboles avec une asymptote à y = 1. |
|||
|
Graphes
|
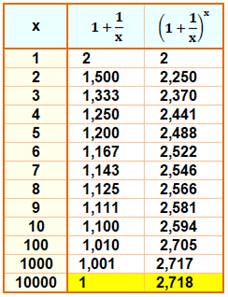
Tableau de croissance
|
|||
|
Puissance x On constate un tout autre comportement. En positif comme en négatif, il existe une
asymptote y = e. De plus le graphe n'est pas symétrique. Un autre fait
qui montre que cette fonction ne se comporte pas comme celles avec une
puissance constante. |
|
|||
|
Avec des nombres n Calcul de la formule pour différentes valeurs de
n La formule générale est appliquée à notre
fonction |
Développement du binôme à la
puissance n
En rouge,
les coefficient
du binôme. |
|
|
Calcul pour n = 1, 2 et 3
Pour n croissant la valeur de la fonction est
également croissance et en tout cas supérieure à 1 |
||
|
Outils |
|
|
|
|
|
|||
|
Calcul
|
|||
** Niveau supérieur
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Analyse/Limite/UnPunPx.htm
|