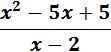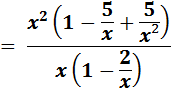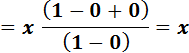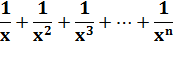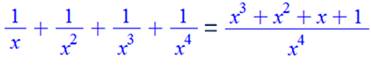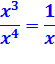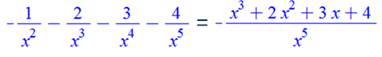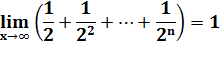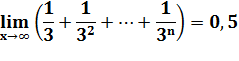NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	ANALYSE
Débutants Général	LIMITES				Glossaire Général
INDEX Analyse Théorie des nombres	Définition	Classique	1 / x, 1 / x² …	Un^Infini
	Dérivées	Polynôme	Hôpital	x . ln (x) …
	Lycée	Sommaire de cette page >>> Approche >>> Somme et produit >>> Division de polynômes >>> Justification >>> Fonction en x^n / x^n^+1

Approche
On sait que x² tend vers l'infini si x devient très grand. Sur l'illustration, on constate que le comportement à l'infini n'est pas affecté si on ajoute des termes de degré moindre. Le terme de degré maximum croît le plus vite et l'emporte nettement sur les autres.	Pour estimer la limite d'un polynôme lorsque x tend vers l'infini, on s'intéresse à son terme de degré le plus élevé.

Somme et produit
Une fonction qui tend vers l'infini ajoutée à une autre fonction qui tend vers l'infini pour x devenant très grand, que fait la somme? Elle tend vers l'infini, naturellement Ce sera vrai pour le produit.	Si Alors

Division de polynômes
Soit la division de deux polynômes telle qu'indiquée sur la figure. x F(x) 10 6,9 100 97,0 1 000 997,0 10 000 9997,0 100 000 99997,0 1 000 000 999997,0 Remarquez que la valeur du polynôme est voisine de x. En effet, pour les grandes valeurs de x: le numérateur se comporte comme x²; le dénominateur comme x; et le tout comme x²/x = x.

Un brin de justification
En mettant en facteur le terme de plus haut degré, on obtient une expression qui permet de comprendre le comportement le l'expression. Le x au dénominateur entraîne la fraction vers 0 lorsque x tend vers l'infini.	Pour x tendant vers l'infini:

Fonction en x^n / x^n^+1
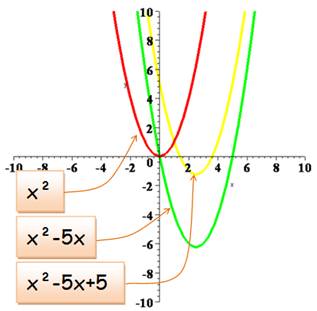
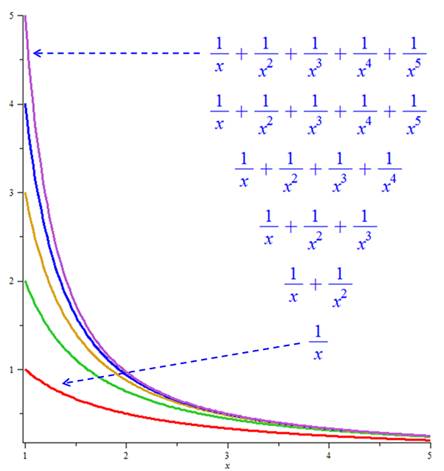
Fonctions en: Le graphe montre qu'elles partent de l'infini pour x = 0 pour converger vers 0 pour x tendant vers l'infini.
Avec mise au même dénominateur ces fonctions s'écrivent, par exemple:
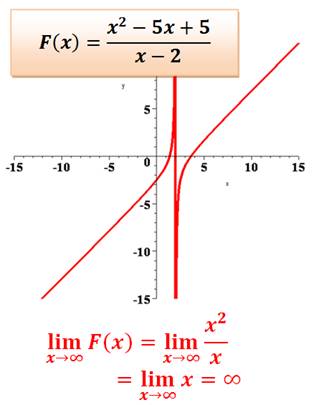
La fonction se comporte bien comme le monôme quotient des monômes de degrés les plus forts au numérateur et au dénominateur.
Pour information la dérivée de cette fonction.
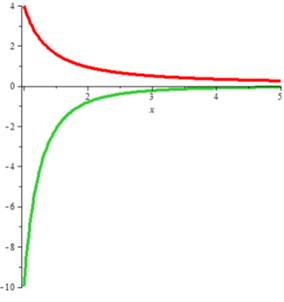
Et les graphes de la fonction et de sa dérivée.
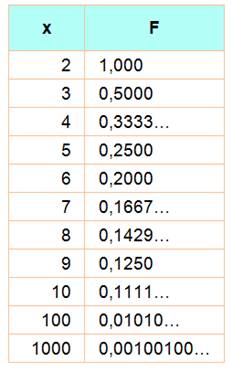
Valeurs numériques Pour x = 2, convergence vers 1. Pour x = 3, convergence vers 1/2. Notez bien les deux formes de convergences pour chaque valeur de x avec n tendant vers l'infini (tableau ci-contre); et pour x tendant vers l'infini: le bas du tableau à poursuivre jusqu'à l'infini.

Voir Séries en 1/ (1-x)

Suite	Règle de l'Hôpital Limite de 1/x et semblables
Voir	Limite – Glossaire Dérivées Identité d'Euler
Aussi	DicoMot Débutants
Cette page	http://villemin.gerard.free.fr/aMaths/Analyse/Limite/Polynome.htm