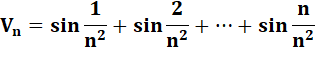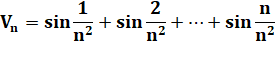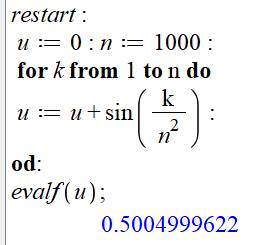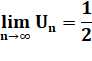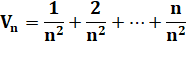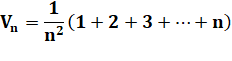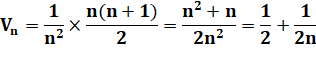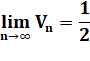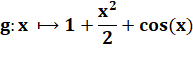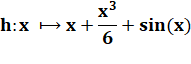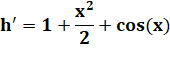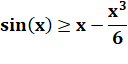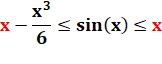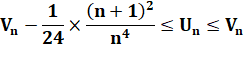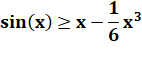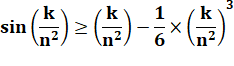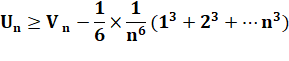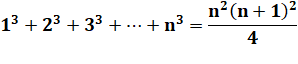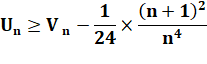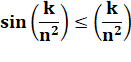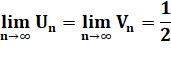NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/09/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	ANALYSE
Débutants Général	LIMITES				Glossaire Général
INDEX Analyse Théorie des nombres	Définition	Classique	1 / x, 1 / x² …	Un^Infini
	Dérivées	Polynôme	Hôpital	x .ln (x)
	Limite avec ln	Sin (k / n²)
		Sommaire de cette page >>> Suite en sinus – Algorithme et programmation >>> Guide de la démonstration >>> Suite simple >>> Encadrement >>> Sommation sur k

Analyse de la suite

qui converge vers ½ pour n infini

Étude formelle pas à pas avec au préalable une vision expérimentale (algorithme et programmation).

Suite: Un=sin(1/n^2)+sin(2/n^2)+...+sin(n/n^2)
Étude expérimentale de la suite	n est un entier strictement positif
Programme Maple	Algorithme (commentaires) Se mettre en situation de départ. Mettre u à 0 et fixer n à 1000. Lancer une boucle de calcul avec k allant de 1 à n. Calculer le nouveau terme de la suite (sin(k/n²) et l'ajouter à la valeur de la suite u déjà calculée. Fin de la boucle (od = do à l'envers). Évaluez la valeur finale de u et l'afficher (effet du point virgule). La valeur affichée est proche de 0,5 = 1/2
Convergence de cette suite

Voir Programmation

Guide de la démonstration formelle

Suite: Vn= (1/n^2)+(2/n^2)+...+(n/n^2)
Prenons la suite plus simple
Mise en facteur
Somme des entiers
Limite de cette suite

Encadrement de sinus x
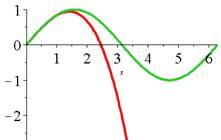
Pré-requis: fonctions qui ne prennent de des valeurs positives sur On étudie la dérivée	Or cosinus(x) est compris entre -1 et +1 => f' est strictement croissante pour x positif. => x est plus grand que sin(x).
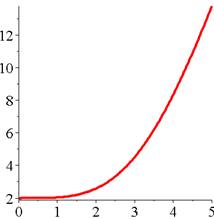
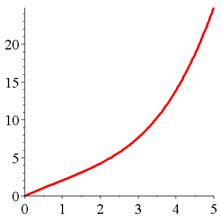
Fonction ayant la précédente pour dérivée	=> g est strictement croissante pour x positif.
Nouvelle fonction ayant la précédente pour dérivée	=> h est strictement croissante pour x positif.
Conséquence pour sin(x). Notez qu'ici, x = n, un entier à partir de 1.	Ex: sin(1) = 0,841… > 0,833... sin(1,57) = 1… > 0,924...
Bilan

Sommation sur k
Nous allons montrer que => Pour tout entier non nul.
Nous avons vu que
Et pour tout k de 1 à n et x = k/n²
En sommant pour les différentes valeurs de k
Notons la somme des cubes.
Ce qui donne
Autre partie de l'inégalité avec x positif
Et pour tout k de 1 à n et x = k/n²
En sommant pour les différentes valeurs de k
Bilan avec les deux inégalités
Notre suite est encadrée par deux suites qui tendent vers la limite de Vn quand n tend vers l'infini

Suite	Voir haut de page Polynômes Un puissance infinie
Voir	Limite – Glossaire Dérivées
Aussi	DicoMot Débutants
DicoNombre	Nombre ½ = 0,5
Cette page	http://villemin.gerard.free.fr/aMaths/Analyse/Limite/Sinkn2.htm