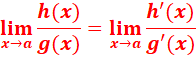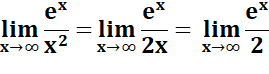NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 28/10/2022

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

   ANALYSE

 

Débutants

Général

LIMITES

 

Glossaire

Général

 

 

INDEX

 

Analyse

 

Théorie des nombres

Définition

Classique

1 / x, 1 / x² …

UnInfini

Dérivées

Polynôme

Hôpital

x . ln (x) …

 

Sommaire de cette page

>>> Limite litigieuse

>>> Règle de l'Hôpital

>>> Exemple

 

 

 

 

Règle de l'Hôpital

 

Comment trouver certaines limites qui semblent indéfinies ?

Une première approche.   

 

 

Limite litigieuse!

 

*    Nous nous intéressons à la division de polynômes donnant la fraction 0 / 0.

*    Que faire?

*    L'intuition nous dit de nous intéresser à la vitesse de variation du numérateur comme à celle du dénominateur. Qui va le plus vite?

*    Bonne idée, et en maths, la vitesse c'est la dérivée.

 

Exemples

Facile!

Mais que dire de:

lorsque x tend vers 1:

Horreur!

 

Voir Zéro et infini

 

 

 

Règle de l'Hôpital

 

*    Dans les cas d'indétermination de la limite du type:  ou encore  et dans ces cas uniquement:

 

 

*    Dans le cas où, on se retrouverait à nouveau dans un cas d'indétermination, on recommence en dérivant une nouvelle fois.

 

Explicitement, cela veut dire que la division des dérivées se comporte comme la division des fonctions.

 

Coin matheux:

Soient f et g deux fonctions réelles continues dans l'intervalle ]-h,+h[, dérivables, sauf peut être en 0, dans cet intervalle, et telle que g(x)  0 pour x  0. Si f(0) = g(0) et si

alors

Anglais: L'Hôpital's rule or Bernoulli's rule

 

Guillaume de l'Hôpital (1661-1704), marquis de Sainte-Mesme.

Mathématicien français.

1696 – Traité sur l'analyse des infiniment petits pour l'intelligence des lignes courbes; premier manuel de calcul différentiel.

 

Ne pas confondre avec

Michel de l'Hôpital (1505-1573), chancelier français.

Médiateur durant les guerres de religion.

Voir Années 1600

 

 

 

Exemple

 

*    L'expression de départ =>

 

*    La dérivée du numérateur et celle du dénominateur (pas la dérivée de la division, qui serait beaucoup plus compliquée!)

*    On cherche ce qui se passe pour x = 1

 

 

 

Tableau

x                          f(x) / g(x)

-4                               1,67  

-3                               1,50  

-2                               1,00  

-1                             DIV/0

0                                3,00  

0,6                              2,63  

0,8                              2,56  

0,9                              2,53  

0,95                          2,513  

0,99                          2,503  

0,999                       2,5003  

0,9999                   2,50003  

0,99999                2,500003  

1                                DIV/0

1,00001                2,499998  

1,0001                   2,49998  

1,001                       2,4998  

1,01                          2,498  

1,05                          2,488  

1,1                              2,48  

1,2                              2,45  

1,4                              2,42  

2                                2,33  

3                                2,25  

4                                2,20  

5                                2,17  

 

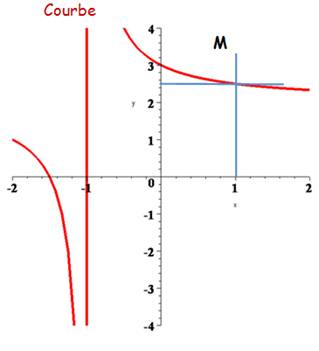
Le phénomène est curieux car

-      la courbe semble continue autour de x = 1

-      pourtant, en 1 précisément la division est indéterminée (0/0)

 

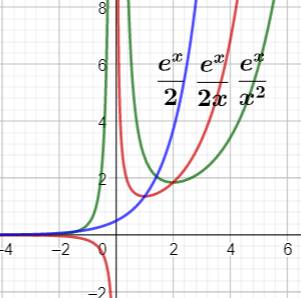
Exemple de double dérivation

 

 

 

 

 

 

 

 

Suite

*    Polynômes

*    Un puissance infinie

Voir

*    Limite – Glossaire

*    Dérivées

*    Hôpital Villemin

Aussi

*    DicoMot

*    Débutants

Sites

*   Règle de l'Hôpital – Wikipédia

*  L'Hôpital's rule – Math is fun

Cette page

http://villemin.gerard.free.fr/aMaths/Analyse/Limite/Hopital.htm