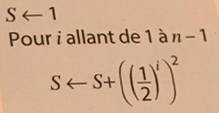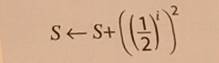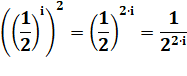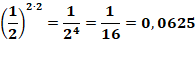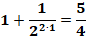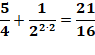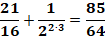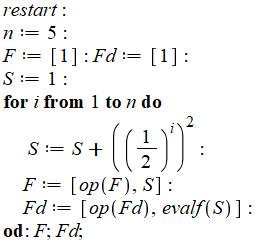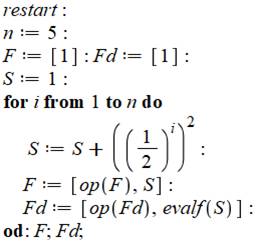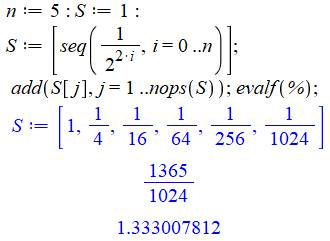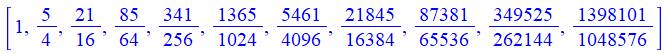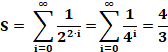|
||||||||||||||||||||||||||||||||
|
PROGRAMMATION PYTHON Un exercice expliqué pas à pas Je suis perdu comme une poule qui aurait trouvé
un couteau ! J'ai vraiment besoin
d'une explication qui reprenne tout depuis le début.
|
Voir absolument Mon espace de travail
en Python
|
|
||
|
On nous
demande de déchiffrer cet algorithme. Comment
le lire, l'interpréter et le réaliser en langage Python ? |
|
|
|
Mentalement, on lit les lignes les unes après les
autres. Chaque ligne est un code, une instruction, une directive invitant à
effectuer un calcul, une opération, un traitement. |
||
|
Première ligne Notation classique avec une flèche d'une fonction à laquelle on attribue une
valeur, on affecte une valeur Ici, on indique que la variable S va prendre la
valeur 1. En Python, c'est simple: on écrit S = 1; dans d'autres
langages de programmation, on précise bien qu'il s'agit du chargement de la
valeur 1 dans un mémoire que l'on appelle S, et on écrit: S: = 1. Il est probable que cette variable va être
modifiée au cours du déroulement de l'algorithme. On dit que cette ligne est
une instruction d'initialisation. |
La variable S prend
la valeur 1. On note: S
= 1 ou parfois: S
:= 1 |
|
|
Deuxième ligne Cette ligne de code est typiquement une
instruction de répétition de tout le calcul qui va suivre. On dit qu'il s'agit
d'une boucle de calcul ou aussi qu'il
s'agit d'un calcul itératif (qui veut
dire: répétitif mais avec des valeurs qui changent à chaque fois). Ici, on lit
qu'il faut faire le calcul (n – 1) fois avec une variable i qui va
prendre les valeurs successives de 1 à n – 1 On remarque en passant que l'algorithme ne
précise pas la valeur de n; elle est laissée au choix de l'utilisateur. |
Si n = 4 Alors: i = 1, puis, 2, puis 3 et Arrêt car 4 – 1 =
3 |
|
|
Troisième ligne Nous avons la signification de la flèche: ici, la
variable S va être modifiée. Sa nouvelle valeur est égale à l'ancienne valeur
à laquelle on ajoute cette drôle de fraction. Coin maths La fraction est égale à 1/2 = 0,5 portée d'abord
à la puissance i (qui au début vaut 1) et, le tout, au carré. En fait, cette
double puissance (i puis 2) se résume à une seule (2i) Le numérateur (1) à la puissance 2i vaut 1 et le
dénominateur vaut 2^2·i. L'accent circonflexe (^)
est le symbole de la puissance lorsqu'on se peut pas écrire les exposants. En
informatique (Python) on utilise aussi le double astérisque: ** |
|
|
Retour à l'algorithme complet Appel avec n = 4. Initialisation avec S = 1. Lancement de la boucle avec i = 1. Premier tour de la boucle n = 3, S = 1 et i = 1: Tour suivant avec i = 2, Etc. Voir le tableau récapitulatif |
Déroulement le l'algorithme
(boucle)
Arrêt pour i = n – 1 = 4 – 3 Valeur de sortie: 85/64 = 1,328125 |
|
|
|||
|
Algorithme
à réaliser (à implémenter) Si vous
êtes novices en langage Python, il faut absolument lire cette page >>> |
|
||
|
Éditeur (écriture du programme)
Faire enregistrement sous un nom à
vous puis exécution (F5 ou run) Interpréteur (résultat du calcul)
|
Après avoir précisé la valeur choisie pour n, on initialise
la valeur de la somme S à 1. Nous sommes prêts à lancer la boucle. Le code est en anglais et la
ligne se lit: Pour i dans le
domaine (1, n, 1), et implicitement, Domaine (1, n, 1) veut dire: 1 est le départ, n est la valeur
d'arrêt qui, d'ailleurs, ne doit pas être exécutée. Le dernier 1 est facultatif,
il indique que i doit progresser par pas de 1. Le calcul de S s'écrit simplement en retenant que
le symbole de la puissance est **. Si on veut voir le résultat du traitement, il
faut en demander l'impression avec l'instruction print
(imprimer en anglais). Notez qu'en anglais la virgule est devenue un point. |
||
|
|
||
|
Bloc de calcul de la puissance b du
nombre a
Programme principal
|
COMMENTAIRES Puissance b de a: création d'une
fonction Curieusement Scratch ne dispose pas du calcul de
la puissance. Le premier programme est un bloc,
défini à l'aide de la palette des instructions. Ce bloc dispose de deux valeurs d'entrée a et b
et va multiplier a par lui-même b fois, le résultat est dans P. Le programme principal commence par initialiser
n = 10 (exemple), S = 1 et place i, un compteur de boucle, à 1. Les résultats du calcul seront placés dans la
liste L, en commençant avec le premier élément 1. Boucle de répétition On positionne a et b pour appeler la fonction Puissance, laquelle livrera son résultat en P. Cette valeur est injectée dans le calcul de S, et
le résultat est ajouté à la liste L. Avant de repartir pour une nouvelle itération, la
valeur de i est incrémentée (on lui ajoute 1). Résultat du calcul Le programme est lancé en cliquant sur le drapeau
vert. La liste calculée est visible dans la zone d'exécution.
Au besoin, le cadre est redimensionné
en l'étirant en bas à droite. La dernière instruction "attendre une
seconde" est facultative. Elle permet de voir se constituer la liste pas
à pas.
|
|
|
|
||
|
Programme
Résultat
|
Explications Restart efface tout ce
qui a pu être fait auparavant. On donne une valeur à n
et à S au démarrage. On introduit deux listes de nombres (F et Fd) pour
recueillir tous nos calculs. La boucle se lit: pour i de 1 à n faire. La
boucle sera close en écrivant le do (faire)
à l'envers: od. Calcul de S. Ce langage dédié aux maths permet
l'écriture classique de la formule mathématique. On range le résultat sous sa forme fractionnaire
dans F, puis sous sa forme décimale dans Fd (instruction evalf). En écrivant F; et Fd;
le programme imprime ces deux listes. |
|
|
Programme pour expert
|
Explications Initialisation Calcul de tous les inverses des puissances de 2
dans la séquence S. On commence par i = 0 pour disposer du 1 initial. Addition de toutes des valeurs avec add. Les valeurs sont extraites de S pour les rangs
j allant de 1 au dernier spécifié par nops(S). Les points virgules indiquent que les résultats
doivent être imprimés. |
|
|
Encore plus concis
|
Algorithme traduit en formule
Lecture: S est
égal à la somme cumulée de cette expression pour i valant toutes les valeurs
de 0 à n. L'instruction sum
opère directement ce type de calcul (somme cumulée). |
|
|
S est la somme cumulée des inverses des
puissances paires de 2: Fractions
Expression décimale (en gardant le
point anglais) 1, 1.250000000, 1.312500000, 1.328125000,
1.332031250, 1.333007812, 1.333251953, 1.333312988, 1.333328247, 1.333332062,
1.333333015 Convergence Cette suite de nombres converge vers 1, 333… = 4/3 Algorithme traduit en formule
|
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
