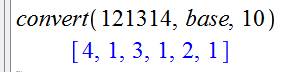|
|||||||||||||||||||||||||||||||||||||
![]()
|
Extraire les chiffres d'un nombre Procédure pas à pas Plusieurs possibilités: |
||
|
Pas à
pas Extraction des unités, puis des
dizaines, etc. Programmation la plus simple
possible. à voir comme exercice de programmation. |
Algébrique Extraction directe par évaluation
d'une expression algébrique (une formule). Programmation avec instructions avancées
de sommation. |
Instruction
dédiée Extraction par conversion en base 10. Programmation avec instructions
prévues pour (dédiées). |
Formule donnant la quantité de chiffres d'un
nombre
|
La quantité de chiffres dans un
nombre entier est égale à la valeur
plafond du logarithme décimal.
Ne pas utiliser
qui est faux pour les puissances de 10 |
Remarque
|
Avec toutes les connaissances que nous avons, nous allons
extraire les chiffres,
un à un, d'un nombre. Il
s'agit d'un exercice de programmation. Car, avec Maple, et sans
doute avec la plupart des logiciels mathématiques, on obtient immédiatement
les chiffres d'un nombre en faisant une conversion
à base 10.
Voir Développements |
Voir Redondance
pour comparaison avec les chiffres
Pour extraire les
chiffres avec un tableur, voir algorithme Kaprekar
|
|
||
|
|
> n:=12345: irem(n,10); n:= iquo(n,10):irem(n,10); (etc)
> C:=[]: n:=12345: n:= iquo(n,10):
C:=[op(C),irem(n,10)]; (etc)
> C:=[]: n:=12345: for i from 1 to 5 do C:=[op(C),irem(n,10)]; n:= iquo(n,10): od: C;
> C:=[]: n:=12345789654: while n>0 do C:=[op(C),irem(n,10)]; n:= iquo(n,10): od: C;
|
|
|
|
||
|
|
> C:=[]: n:=854976213845: while n>0 do C:=[op(C),irem(n,10)]; n:= iquo(n,10): od: sort(C);
Transformer la liste [ ] en un ensemble { }
élimine les doublons >>> |
|
|
|
||
|
|
> # Extraction des chiffres C:=[]:
n:=123456789:
while n>0 do C:=[op(C),irem(n,10)]; n:= iquo(n,10):
od: # calcul de la somme des chiffres
S:=0: for n from 1 to nops(C) do S:= S + C[n]: od: S;
|
|
|
|
||
|
Ri
= Cq – i + 1
|
> restart: C:=[]: n:=8549762: while n>0 do C:=[op(C),irem(n,10)]; n:= iquo(n,10): od: q:=nops(C): for i from 1 to q do R:=[op(R), C[q-i+1]] od: R;
|
|
|
Chiffres des carrés |
|
|
|
|
> restart: for
N from 10 to 20 do n:= N*N: C:=[]: while n>0 do C:=[op(C),irem(n,10)]: n:= iquo(n,10): od: q:=nops(C):R:=[]: for i from 1 to q do R:=[op(R),C[q-i+1]] od: lprint(N,R): od: 10, [1, 0, 0] 11, [1, 2, 1] 12, [1, 4, 4] 13, [1, 6, 9] 14, [1, 9, 6] 15, [2, 2, 5] 16, [2, 5, 6] 17, [2, 8, 9] 18, [3, 2, 4] 19, [3, 6, 1] 20, [4, 0, 0] |
|
|
|
> restart: for
N from 3 to 100 do n:=
N*N: C:=[]: while n>0 do C:=[op(C),irem(n,10)]: n:= iquo(n,10): od: q:=nops(C):R:=[]: for i from 1 to q do R:=[op(R),C[q-i+1]] od: if
C[1]=4 and C[2]=4 then lprint(N,R): fi: od: 12, [1, 4, 4] 38, [1, 4, 4, 4] 62, [3, 8, 4, 4] 88, [7, 7, 4, 4] |
|
|
> restart: for
N from 3 to 1000 do n:= N*N: C:=[]: while n>0 do C:=[op(C),irem(n,10)]: n:= iquo(n,10): od: q:=nops(C):R:=[]: for i from 1 to q do R:=[op(R),C[q-i+1]] od: if
C[1]=4 and C[2]=4 and C[3]=4 then r:= cat(op(R)): print(r); fi: od:
|
|
Astuce: Une instruction
suivie de ";" indique que le
résultat doit être imprimé. Avec ":",
le calcul est muet. L'instruction print joue le même rôle que le ";": elle restitue les fractions et les
formules. L'instruction
lprint imprime le même résultat mais en linéaire. Exemple: > ConstantePi:=
3,14159:Phi:=(sqrt(5)+1)/2: print(ConstantePi,Phi): lprint(ConstantePi,Phi):
3, 14159, 1/2*5^(1/2)+1/2 |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()