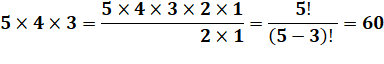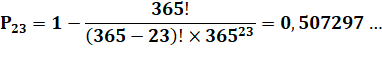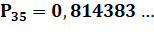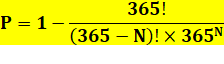![]()
|
|
Ce site
est désormais accessible en http://diconombre.fr/index.html et pour cette page voir le lien en fin de page For this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||
![]()
|
ANNIVERSAIRES Le paradoxe des anniversaires Combien de personnes ont le même
anniversaire parmi: -
les
élèves d'une classe, -
les
présidents de la République, -
les
députés, -
les rois
de France, -
les
cosmonautes, -
les
moines de telle abbaye, -
… Dès l'inst on a plus
d'une chance sur 2 de trouver deux personnes nées le même jour. (pas forcément la même année). |
Anniversaires
identiques
Charles
IX est né le 27 juin. Louis
XII est né le 27 juin.
Harding
est né le 2 novembre. Polk est né le 2 novembre.
Albert
IV est né le 21 septembre. Frédéric
IV est né le 21 septembre. Charles
V est né le 24 février. Matias est né le 24 février.
Aucun
n'a le même anniversaire. Selon
Albert Jacquard |
Anglais: the
birthday problem
Voir Paradoxes
Premier cours introduction aux probabilités
|
Dans
une classe d'une trentaine de personnes, le prof demande la date de naissance
au premier élève et questionne les autres pour savoir si l'un d'entre eux est
né ce jour là de l'année. Sinon, il continue avec les élèves suivants. Il est
pratiquement sûr de réussir ce qu'il cherche: trouver deux élèves ayant la même date de naissance. Les élèves sont
étonnés et le prof ravi de son coup. |
Quelques probabilités avec les anniversaires
|
P en % |
Qté |
OUI/NON |
Même
date d'anniversaire |
|
50 |
23 |
OUI |
Parmi 23 personnes, il y a 1 chance sur
2 de trouver deux personnes ayant la même date anniversaire. |
|
100 |
366 |
OUI |
Nées
le même jour (ou 367). |
|
50 |
253 |
OUI |
Même
anniversaire un jour donné. |
|
0,2739… |
2 |
OUI |
Il y a 0,27 % (= 1/ 365) de
probabilité que deux personnes aient la même date d'anniversaire. |
|
99,726… |
2 |
NON |
|
|
0,00075… |
3 |
OUI |
|
|
99,9992… |
3 |
NON |
|
|
|
|
|
Une chance sur deux de trouver au moins* deux
personnes ayant le même anniversaire parmi 23 personnes. * Au moins deux, mais la probabilité d’en avoir
trois ou plus est très faible.
|
|
|
|
||
|
Anniversaire
de mon copain
|
||
|
|
1 possibilité sur
365 |
|
|
|
? |
|
|
|
364 possibilités
sur 365 P2différents
= 364/365 |
|
|
|
? |
|
|
|
P2identiques
= 1 – P2différents = 1 – 364/365 = 1/365 = 0,0027 => 0,27 % |
|
|
|
||
|
|
|||
|
|
1
– (364/365) = 0,003 => 0,3 % (0,2739…) |
||
|
|
1
– (364/365) (363/365) = 0,01 => 1 % (0,8204…) |
||
|
|
1
– (364/365) ... (357/365) => 0,09 => 9 % (9,4623…) |
||
|
|
Note de calcul pour l'établissement de la formule
Voir Factorielle |
||
|
Formule
Tableau
Graphe Environ: 50 % de probabilité pour 23
personnes & 81 % avec 35 personnes
|
|||
|
Problème de l'anniversaire
adjacent |
|
|
Problème de l'anniversaire adjacent: il faut seulement 14 personnes pour avoir
deux personnes avec anniversaires adjacents
avec une probabilité de 50%. Avec 30 personnes, la probabilité est proche de
98%. Problème
résolu en 1970: Ref Wolfram:
The "almost" birthday problem, which asks the number of people
needed such that two have a birthday within a day of each other, was
considered by Abramson
and Moser (1970), who showed that 14 people suffice. Ces
auteurs proposent le tableau suivant:
Exemples:
k = 1 et p = 24 => avec 23 personnes la probabilité du même jour anniversaire est 0,50729; avec k
= 2 et p = 14 => avec 14 personnes la probabilité d'avoir un anniversaire
adjacent (à un jour près) est 0,53749. |
|
Merci
à A. Clement pour ses
remarques
Calcul général et approximations
|
Le problème des
anniversaires est un cas particulier du problème général suivant: Soit n balles lâchées
au hasard sur k cases ( La probabilité qu'il n'y
ait pas plus d'une balle par case (pas deux balles ou plus par case) est
(avec approximation pour n petit par rapport à c):
Probabilité pour avoir
au moins une fois deux balles dans la même case: P = 50% pour Avec k = 365 jours, on
retrouve bien n = 22,92… pour P = 50%. Cas de balles
dans plusieurs casiers (c1, c2, .. ck) ou de
personnes ayant le même anniversaire ou ayant
le même jour de fête ou le même ticket gagnant à la loterie ...
Cas du même
anniversaire ou de la même fête: il faut 16 personnes dans une assemblée pour
obtenir un des événements avec 50% de chance, et 34 pour 95%. |
Source: Methods for Studying Coincidences >>>
Remarque morbide …
|
Parmi
23 personnes, la probabilité de trouver deux personnes nées le même jour est
de 50 %; c'est aussi la probabilité que deux personnes soient décédées
le même jour, pas de la même année. |
|
|
|||
|
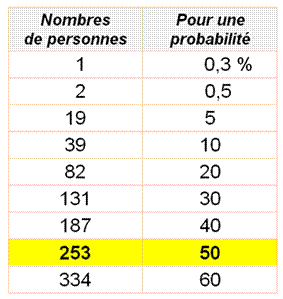
Il faut 253 personnes pour trouver parmi elles,
une personne ayant le même anniversaire que vous avec une chance sur deux. Exemple
avec le 14 juillet (vrai pour toute autre date) |
|||
|
|
364/365 |
||
|
|
1–
364/365 = 0,003 => 0,3% |
||
|
|
1
– (364/365)² = 0,005 => 0,5% |
||
|
|
1
– (364/365)23 = 0,061 => 6,1% |
||
|
|
1
– (364/365)253 = 0,5 => 50% |
||
|
|
|
||
|
|
|
||
|
|
|||
![]()
|
|
|||
|
Question Ma mère et mon
père ont le même jour anniversaire:
Quelle est la
probabilité d'une telle coïncidence? |
Théorie et réalité D'une manière générale, quelle est la probabilité
de deux anniversaires le même jour pour deux personnes données ? Calcul théorique, hors phénomènes sociaux.
|
||
|
Naissance
le même jour La probabilité
que mon père soit né le jour anniversaire de ma mère est: P1 = 1 – (364/365) =
1/ 365 Décès le
même jour La probabilité
que mon père soit décédé le jour anniversaire du décès de ma mère est: P2 = 1 – (364/365) =
1/ 365 Nature
des événements La naissance et
la mort étant des événements qui se succèdent mais qui surviennent n'importe
quand (sans que l'un soit lié à l'autre), les probabilités sont indépendantes
et se multiplient: P = (1/365)² = 1/ 133
225 |
Commentaire Cette probabilité s'applique à
quiconque partage le même jour anniversaire que moi. La probabilité que ce
soit le cas est bien 1/365. Et, alors, la probabilité, ayant trouvé cette
personne, qu'elle décède le même jour que moi est à nouveau 1/365. Ce peut être
ma mère, ma sœur ou un quidam. Il se trouve que cette infime chance
s'est matérialisée avec mon père et ma mère, comme s'ils avaient tous deux
gagnés au loto sans qu'ils se soient
concertés. Analogie Le destin a pris une route sur 365
pour faire que mon père partage le même anniversaire que ma mère. Puis, le
destin a poursuivi sa route et a pris un chemin sur 365 pour fixer la date
finale. Soit sur le parcours, un chemin parmi 365 x 365. |
||
|
Cas de
trois personnes partageant deux dates anniversaires P = (1/365)4
= 5,6 10-11 |
Cas d'une personne décédée le jour de son anniversaire La probabilité
théorique de mourir le jour de son anniversaire est 1/365. Mais … Il
semble que la mortalité est plus importante le jour de son anniversaire que
n'importe quel autre jour (14%). Le stress de l'année en plus ? L'effort de
tenir jusque là ? Suicides dus au blues de l'anniversaire ? Personnages
célèbres morts le jour de leur anniversaire : William Shakespeare, Raphael,
Franklin Roosevelt, Ingrid Bergman, Sidney Bechet, Mike Douglas … |
||
Anglais: Probability that two given
people share the same birthday and the same date of death
Étonnant !
|
Si on considère un groupe de 250 personnes d'une
société où les employés ont entre 18 et 68 ans (plage de 50 ans), la
probabilité que deux d'entre elles soient nées le même jour (jour/mois/an)
est de 81%. Si on prend au hasard 1000 personnes ayant vécu
les mille dernières années, la probabilité que deux d'entre elles soient nées
le même jour (jour/mois/an) est de 74%. |
Merci à Joseph Dimijian pour ces calculs
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()