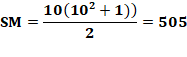Carrés magiques d'ordre 10, construction

Comment profiter de la construction d'un carré magique 5x5 (impair, réputé simple à construire) pour façonner un carré 10x10 (pair, généralement plus compliqué à construire).

Il est conseillé de voir d'abord l'explication pour

la construction du carré 6x6 à partir d'un 3x3.

Un carré magique 5x5

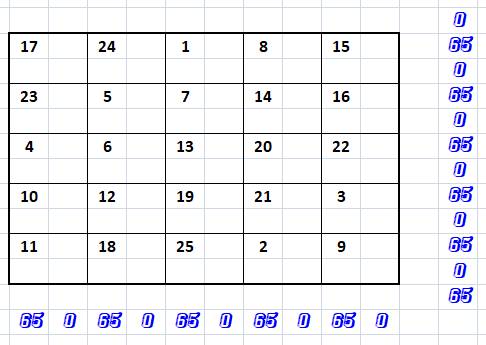
Le carré 5x5 est construit dans un canevas de 10x10.

On retrouve la méthode classique de construction:

montée en diagonale et enroulement au delà des bordures

descente d'un cran aux multiples de 5.

Un carré initial 10x10
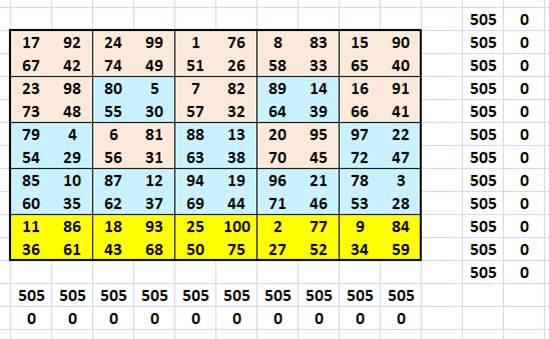
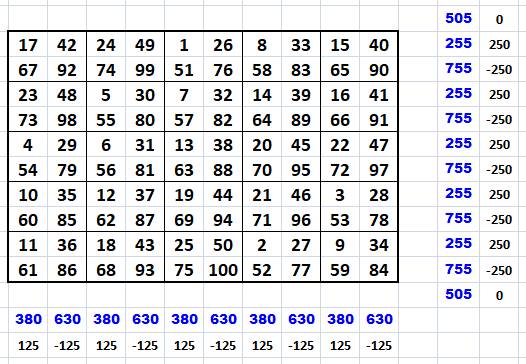
Le carré 5x5 initial est répété quatre fois avec les nombres de 1 à 100 La somme magique vaut: Cette construction simple s'approche de la solution: écart alterné de 250 sur les lignes; écart alterné de 125 sur les colonnes; et sommes correctes sur les diagonales.	Chaque zone 2x2 est complétée par trois nombres augmentés de 25. En bleu la somme des lignes, colonnes et diagonales. À côté, les écarts par rapport à la somme magique.
Idée ? Permuter les nombres dans les zones 2x2.	On se dit que la solution est à portée de main. Pas si sûr ! Une simple permutation générale dans les zones 2x2 ne parvient pas à contribuer de 25 par zone en colonne (125/5) et de 50 par zone en ligne (250/5). Il faut procéder à des permutations sélectives.

Une solution 10x10
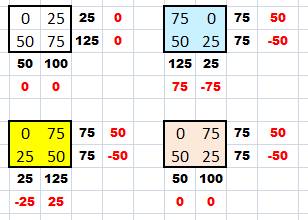
L'astuce de construction Voici quatre permutations d'une zone 2x2 avec l'originale en blanc. On a indiqué les écarts. En prenant les nombres en croissants: en jaune, on a une disposition en U; en bleu, une disposition en U inversé; et en marron, une disposition en croix. Les nombres latéraux en rouge indiquent quelle est la variation par rapport à la zone originale en ligne comme en colonne. Par exemple, en optant pour une disposition en U (jaune), on ajoute 50 sur les lignes et on retranche 25 sur les colonnes. *Reste à réfléchir à un jeu de "pesée" pour combler les écarts.*		Les quatre permutations utilisées En utilisant les écarts produits par ces permutations, il s'agit de les sélectionner pour atteindre les différences en ligne et en colonne du carré magique complet.
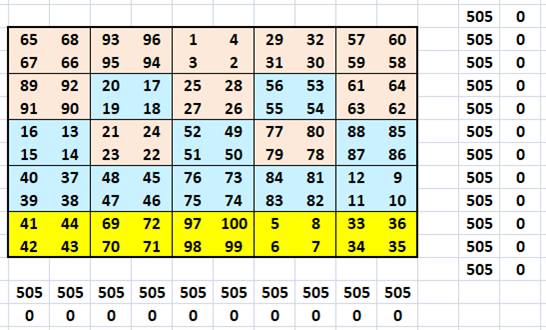
Une des solutions Cette sélection des permutations de zone 2x2 résout le problème des écarts et produit un carré magique 10x10. Si vous essayez une autre combinaison, n'oubliez pas de surveiller les diagonales.