|
||||||||||||||||||||||||||||||||||
|
Énigmes avec calculs Quelques devinettes
typiques. Parfois déroutantes … |
Devinettes pour se chauffer (niveau 6e)
|
Nous
avons chacun la même somme d'argent. Combien dois-je te donner pour que tu
aies 20 euros de plus que moi? |
|
Au
marché, j'ai remarqué que 4 pommes et 3 bananes valent 15 euros. Et, en
inversant, 4 bananes et 3 pommes ne coûtent que 13 euros. Quel est le prix unitaire
de chaque fruit? |
|
|
||
|
Énigme Nathan
est adepte de cyclisme, une fois par semaine. Il se donne un défi: faire 25
km de plus chaque semaine durant six semaines. En fin d'entrainement son
compteur indique 675 km. Combien
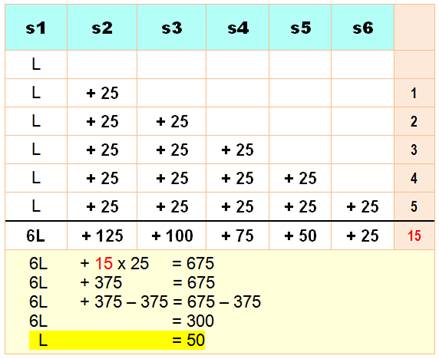
a-t-il parcouru de kilomètres la première semaine ? Solution Un petit
tableau va aider à faire le calcul. La première semaine, il roule sur une distance encore inconnue, disons
L kilomètres. La deuxième semaine, il parcourt la même distance plus 25 km (L + 25). La troisième, encore la même distance (L + 25), prolongée de 25 km
soit L + 25 + 25. Etc. |
|
|
|
Calcul La colonne rose à droite
récapitule combien de fois il parcourt les 25 km en plus. |
15 fois 25 km en plus = 375 km |
|
|
À la fin de l'entraînement,
il aura parcouru: |
6 fois la distance initiale L et 375 km
supplémentaire pour une indication compteur de 675 km 6L + 375 = 675 |
|
|
Comment trouver L enfoui
dans cette égalité? |
Une égalité ressemble à une balance:
l'équilibre doit être maintenu. |
|
|
Je retranche la même
quantité de chaque côté |
6L + 375 – 375 = 675 – 375 6L = 300 |
|
|
Je divise les deux côtés par
6 |
L = 50 km |
|
|
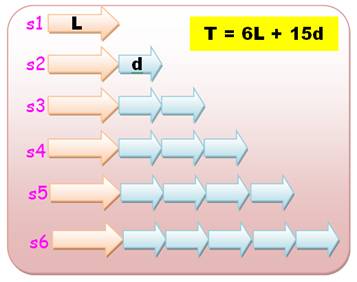
Résumé en figure Le trajet total (T) est égal
à six fois la distance initiale augmentée de quinze fois le supplément hebdomadaire Et, en route vers l'algèbre
…
Voir Je
me lance à calculer des équations |
|
|
|
LE COCKTAIL |
|
|
|
Voici un mélange. |
1 volume
à 12° 2 volumes à 8° 1
volume à 16° |
|
|
Calculer son degré d'alcool (d) |
Le mélange est formé de 4 volumes en tout. Un degré d'alcool exprime en fait un pourcentage: 1 degré d'alcool =
1% d'alcool pur. 100 x 4 d.v = 12 v + 2 x 8 v + 16 v
400 d = 44 d = 0,1 ou 11° |
|
|
|
|||
|
Voici une distribution de
bonbons. |
437
bonbons en tout. Le premier enfant reçoit p bonbons. Le 2e en a 2 en moins. Le 3e encore 2 en moins. Etc. |
||
|
Trouver la valeur de n, le
nombre d'enfants? Trouver d, le nombre de
bonbons que reçoit le dernier enfant? |
L'énigme est basée sur le fait que les facteurs
premiers de 437 sont 19 et 23. |
||
|
Calcul pour chacun en
commençant par le dernier. |
Dernier Avant-dernier … 2e 1er |
d d + 2 (1) … d + 2 (n – 2) d + 2 (n – 1) = p |
|
|
avec la somme
des entiers jusqu'à n. |
Total = 437 |
= n.d + 2 {n (n – 1)} / 2 = n.d + n (n – 1) = n (d + n – 1) |
|
|
Propriété de 437. |
Or 437 = 19 x 23 |
= n (d + n – 1) |
|
|
Du fait que n est dans
chacun des facteurs et que l'un doit être plus petit que l'autre. |
n d + n – 1 |
= 19 = 23 |
|
|
Petit calcul. |
d |
= 23 – 19 + 1 = 5 |
|
|
|
|||||
|
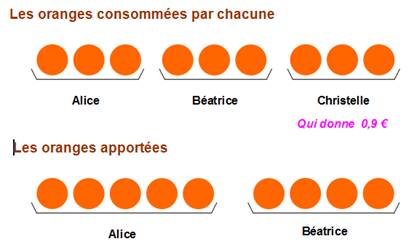
La situation: un goûter |
|
||||
|
La question se pose alors: Combien Christelle doit-elle
donner à chacune des 2 autres ? |
0,5 € à Alice et 0,4 € à
Béatrice NON! Ce n'est pas la bonne
réponse. |
||||
|
Indice
Comment
s'y prendre 1ère
étape - Appréciation de l'apport de Christelle |
|||||
|
|
Alice |
Béatrice |
Christelle |
||
|
Fruits apportés: |
5 |
4 |
|
||
|
Quantité de fruits. |
<= |
5 + 4 = 9 |
=> |
||
|
Soit pour chacune: |
3 |
3 |
3 |
||
|
Contribution de Christelle: |
|
|
0,9 € |
||
|
C'est bien entendu pour obtenir sa part: |
|
|
3 oranges |
||
|
Soit la "valeur" d'un fruit: |
|
|
0,9 / 3 = 0,3 |
||
|
2e étape - Appréciation
de l'apport d'Alice et de Béatrice |
|||||
|
Valeur des fruits consommés: |
3 x 0,3 € |
3 x 0,3 € |
3 x 0,3 € |
||
|
Valeurs des fruits apportés: |
5 x 0,3 € |
4 x 0,3 € |
|
||
|
Différence: |
2 x 0,3 € |
1 x 0,3 € |
|
||
|
Cette différence correspond à ce que ces
deux filles ont cédé à Christelle. |
|||||
|
Christelle doit remettre le montant
correspondant à chacune d'elle. |
0,6 € |
0,3 € |
|
||
|
Ce qui correspond bien à ce que Christelle
a déboursé. |
|
|
0,9 € |
||
|
Bilan Alice apporte 5
oranges et en consomme 3: elle reçoit 0,6 € pour les 2 oranges données à
Christelle. Béatrice apporte 4
oranges et en consomme 3: elle reçoit 0,3 € pour l'orange donnée à
Christelle. Christelle avec ses
0,9 € donne 0,6 € à Alice et donne 0,3 € à Béatrice. |
|||||
Même style: les bières (Explication raccourcie)
|
Cas 1 - Simple Albert
apporte une bière, Bernard en a deux et Constantin arrive les mains vides. Il
propose de mettre 4 euros sur la table pour dédommager ses copains. Quelle
somme revient à chacun. Ce
cas est volontairement simple pour bien comprendre le raisonnement. Albert
vient avec sa bière et la boit. Opération neutre. Bernard boit une bière et
donne l'autre à Constantin. En échange, Constantin donne ses 4 euros à
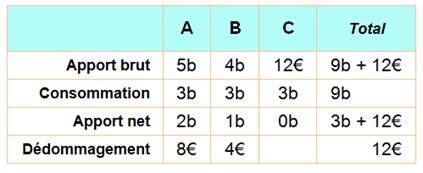
Bernard. Fin de l'histoire. Cas 2 -
Formalisation Albert
apporte 5 bières, Bernard 4 bières et Constantin 12 euros. Voici
le tableau de calcul.
|
|
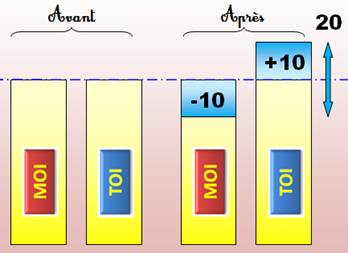
Problème Nous avons chacun la même somme d'argent.
Combien dois-je te donner pour que tu aies 20 euros de plus que moi? Solution Il suffit que je te donne la moitié (10)
de l'écart demandé pour que cette différence (10) chez moi additionnée à celle
de chez toi (10) crée l'écart voulu (20). |
|
|
Problème Au marché, j'ai remarqué que 4 pommes et
3 bananes valent 15 euros. Et, en inversant, 4 bananes et 3 pommes ne coûtent
que 13 euros. Quel est le prix unitaire de chaque fruit? Solution
|
|
Suite |
|
|
Voir |
|
|
Cette page |
