|
|
Ce site est désormais
accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For this page, refer to the link at the bottom. |
|
22 Novembre
2025
|
Édition du: 14/04/2026 |
|
INDEX |
Triangles entiers |
|||
|
Triangle Héronien de
Fibonacci ou Triangle de Fibonacci Un triangle
héronien est tel que ses côtés et son aire sont des nombres entiers. Il est de
Fibonacci si les longueurs des côtés
sont des nombres
de Fibonacci. Il n'existe
qu'un seul triangle de Fibonacci connu ce jour. |
||
|
|
Sommaire de cette page >>> Triangle de
Fibonacci >>>
Presque-Triangle de Fibonacci |
Débutants Glossaire |
Anglais: Fibonacci triangle
|
Nombre de Fibonacci Les
25 premiers nombres 1,
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,
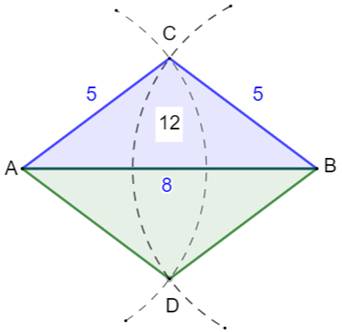
6765, 10946, 17711, 28657, 46368, 75025. Exemple (le seul !) Sur
cette figure, chaque triangle est isocèle et les côtés sont des nombres de
Fibonacci successifs (5 et 8). Chaque
triangle est, en fait, un triangle rectangle de Pythagore (3, 4, 5). L'aire
de chaque triangle coloré vaut ½ (3 x 8) = 12. Note:
un tel triangle est avant tout un triangle
entier. Surprise! Les triangles ACB (5, 5, 8) et ACD (5, 5, 6) ont la
même aire: 12. |
Exemple: triangle (5, 5,
8) ou (F5, F5, F6)
|
||
|
Propriétés |
Du
fait de l'inégalité
triangulaire, aucun THF n'est quelconque
(scalène); ils sont tous isocèles. Bien
entendu, il ne peut pas être équilatéral, car un triangle équilatéral entier a une aire irrationnelle Il
existe deux types de THF (avec k > 2)
Thèorèmes Un
TFH du type (Fk, Fk, Fn)
n'existe que pour k = 5 et n = 6 (figure ci-dessus). Un
TFH du type (Fn-k,
Fn, Fn) n'existe pas pour k de 1 à 10. Conjecture:
il n'existe pas d'autres THF que le (5, 5, 8). |
||
|
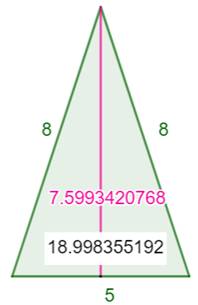
Ce
triangle est surprenant. En
inversant les longueurs du THF vu ci-dessus, on obtient un triangle qui
manque de peu d'être héronien. L'aire
vaut 18,9983… presque 19. Un
autre candidat: le triangle ((2, 2, 144)
avec une aire de 143,9965… Moins
intéressant, car il suffit de conserver le 2 et lui associer un très grand
nombre pour approcher autant qu'on le souhaite une aire à valeur
entière. |
|
|
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |