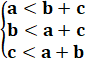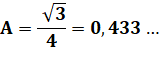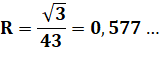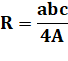|
Édition du: 11/03/2024 |
|
INDEX |
Triangles entiers |
|||
![]()
|
Triangles
à CÔTÉS ENTIERS Triangles
dont les mesures des côtés sont des nombres
entiers. Évidemment son périmètre est un nombre entier. La page
suivante décrit des triangles entiers spécifiques,
des triangles dont d'autres mesures sont
aussi des nombres entiers. Savez-vous
qu'il existe 2024
triangles entiers qui tiennent dans un cercle de 15 cm de rayon ! |
||
|
|
Sommaire de cette page >>> Approche >>> Classement >>> Triangles dans le cercle de rayon 1 >>> Triangles dans le cercle de rayon 2 >>> Statistiques >>> Cas des triangles dans un cercle de R < 15 |
Débutants Glossaire |
|
Recherche des triangles entiers Avec un programme, il est possibles de balayer
tous les nombres entiers pour a, b et c (les côtés du triangle) et de ne
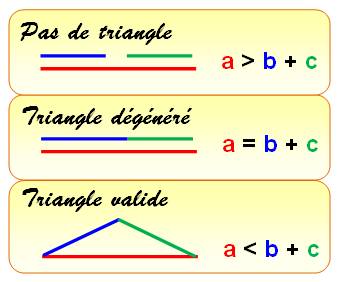
retenir que les triplets qui forment effectivement un triangle. La condition pour qu'un triangle existe est que
chaque côté soit plus long que la somme des deux autres. Sinon, avec deux côtés trop courts, le troisième
sommet n'existe pas. Formellement, pour de vrais triangles, cette inégalité
triangulaire s'énonce:
|
Existence d'un triangle
|
|
|
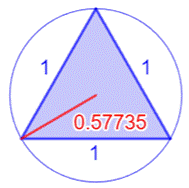
Le plus petit triangle entier C'est le triangle équilatéral de côté unité. Aire du triangle:
Rayon du cercle circonscrit
|
|
|
|
Calcul Si s est le demi-périmètre, formule
de Héron:
et le rayon
du cercle circonscrit:
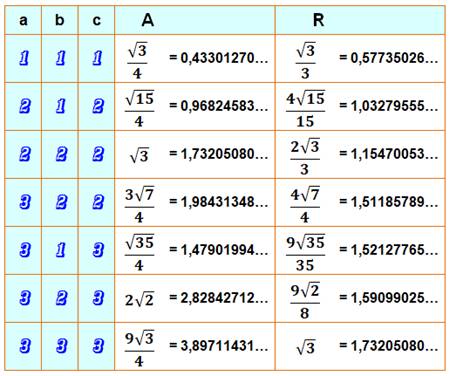
Compter Il faut éliminer les cas de côtés identiques à
une permutation près. Ex: (3, 3, 2) et (3, 2, 3). Un classement par rayon circonscrit croissant ne
marche pas. Il existe des triangles différents avec le même R. Ex: (4, 3, 2) et (4, 4, 2) ont le même R = 8√15/15. En fait, il suffit de maintenir c égal ou supérieur à b
et c'est bon. |
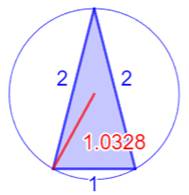
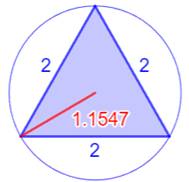
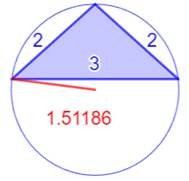
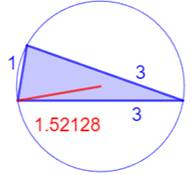
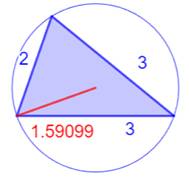
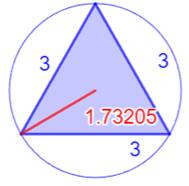
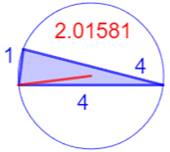
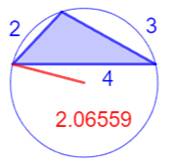
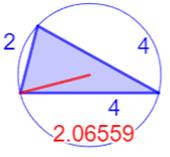
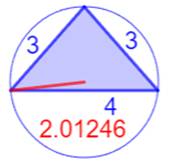
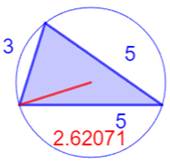
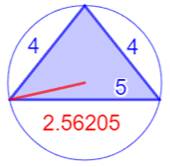
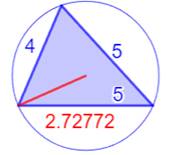
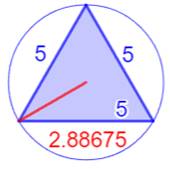
Les sept plus petits triangles
entiers (R < 2)
|
|
Illustration –
Les sept plus petits triangles entiers (R < 2)
|
|
|
|
|
|
|
|
|
|
|
|
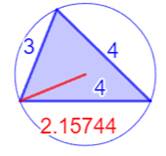
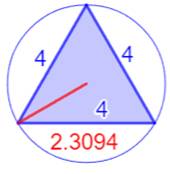
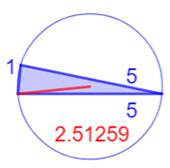
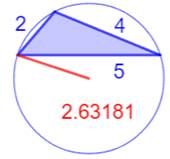
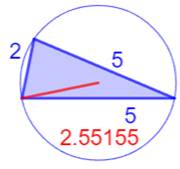
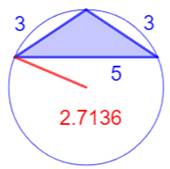
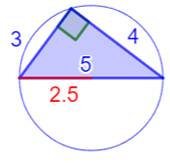
Illustration
– Les quinze plus petits triangles entiers (2 < R < 3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Combien de triangles entiers dans
le cercle de rayon R Pour un rayon 1, il y en a exactement un seul. Pour un cercle de rayon 2, ils sont sept en tout. Pour un rayon 15, ils sont 2024. Voir Les exemples de triangles
ci-dessous |
Quantité de triangle entiers dans
un cercle avec R<n 1, 7, 22, 47, 91, 148, 231, 334, 469, 631, 830,
1062, 1339, 1657, 2024,
2434, 2905, 3427, 4014, 4653, 5362, 6141, 6994, 7911, 8917, 10000, 11169,
12425, 13774, 15211, 16743, 18381, 20133, 21975, 23929, 25998, 28185, 30482,
32906, 35449, 38137, 40935, 43884, 46954, …
OEIS A331229 Rayon correspondant du cercle
circonscrit 0,5773502693, 1,032795559, 1,154700539,
1,511857892, 1,521277658, 1,590990257, 1,732050808, 2,012461179, 2,015810523,
2,065591118, 2,065591118, 2,157439560,
2,309401077, 2,500000000, 2,512594538, 2,551551816, 2,562050461, 2,620712092,
2,631806780, 2,713602101, 2,727723628, 2,886751347, 3,006688972, … |
|
Cas des triangles
contenus dans un cercle de R < 15
|
|
|
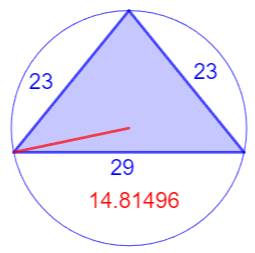
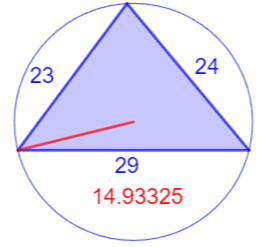
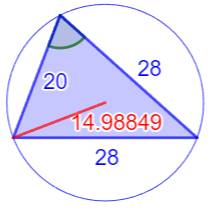
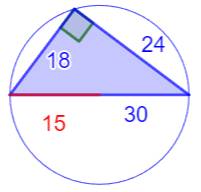
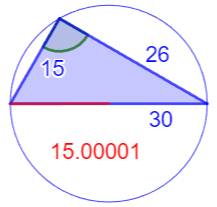
Les trois triangles justes autour
de R =15
Le triangle
du centre est le célèbre (3, 4,
5) x 6
|
|
|
|
Notez que ce n'est
pas forcément les côtés que l'on attendait (autour de 30)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TriaCoEn.htm
|