NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/05/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Géométrie
Débutants Géométrie	VOLUME				Glossaire Géométrie
INDEX Géométrie		Cubes alignés	Boite max	Tétraèdre
	Sommaire de cette page >>> Les 1000 cubes >>> Sur 1 km >>> Calcul >>> Théorie >>> Application: nucléons dans l'Univers >>> Piège à éviter

---

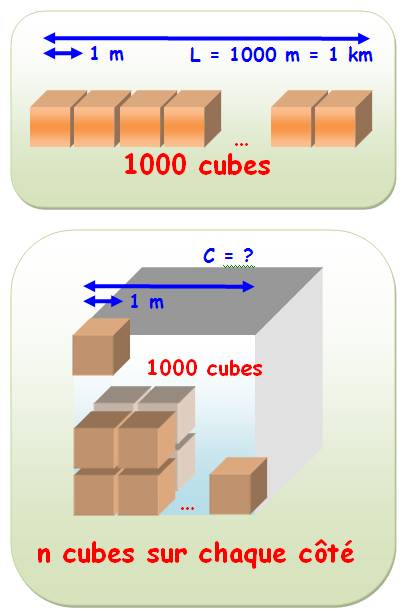
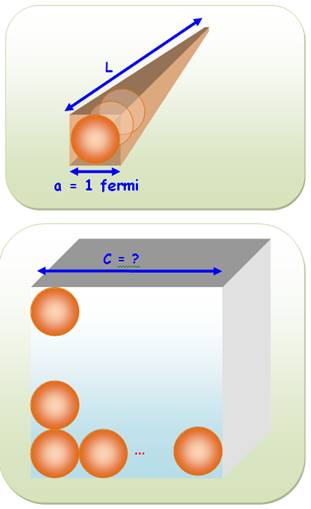
Cubes alignées mis en volume

Soit un alignement de cubes (ou de perles …). Qule est le volume occupé par ces cubes si nous les arrangions en un gros cube?

Attention au piège! Pas si simple!

Pratique des calculs de volume et des conversions des unités.

Les 1000 cubes
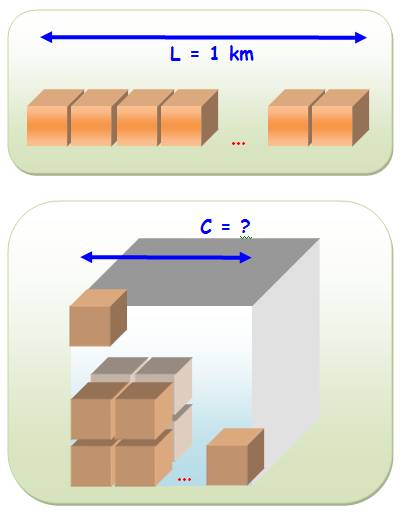
Nous disposons de 1000 cubes, chacun de 1 m de côté. Nous les rangeons de manière à former un gros tas de cubes en forme d'un gros cube. Combien de petits cubes par arête? Avec 2 cubes sur un côté, nous aurons: 2 x 2 x 2 = 2^3 = 8 cubes; loin des 1000 que nous devons arrangés. Avec 5 cubes sur un côté nous aurons: 5^3 = 125 cubes. Avec 10 cubes: 10^3 = 1000. Bingo! n = 10 car 10^3 = 1000 C = 10 x 1 m = 10 m

Sur 1 km
Un alignement de petits cubes qui s'étale sur L = 1 km. Ces cubes sont empilés pour former un grand cube. Quelle est la longueur C du côté du grand cube? Il nous manque clairement une donnée: quelle est la taille du petit cube? Supposons comme ci-dessus que ce côté mesure 1 m. Les mêmes données produisent les mêmes effets: il y a 1000 cubes et mis en gros cube son arête mesure C = 10 m.
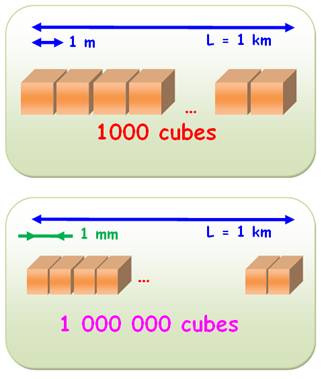
Supposons que nous n'ayons pas vu l'exemple ci-dessus, comment calculer la longueur C de l'arête. Il n'y pas d'autres moyens que de diviser la longueur L en un nombre en puissance de trois: L = C^3 Or L = 1km = 1000 m = 10^3 m Alors C = 10 m Nous aurions pu prendre une autre division, pourvu qu'elle conduiise à une puissance de trois. Exemple L = 1km = 1 000 000 mm = 10^6 mm Alors C = 100 mm Est-ce normal de ne pas trouver la même dimension?

Calcul du volume
L'illustration ci-contre, montre assez bien que, intuitivement, dans les deux cas, nous n'avons pas la même quantité de matière, même si la longueur est conservée (L = 1 km), la section est différente. Calculons le volume dans les deux cas: En haut, en mètres: 1000 x 1 x 1 = 1000 m^3 ou 1000 cubes de 1 m^3. En bas, en mm^3: 1 000 000 x 1 x 1 = 10^6 mm^3. ou 1 million de cubes de 1 mm^3.
Comparons en mm^3 : Unités 1 m^3 = 10^9 mm^3 En haut: 1000 m^3 = 1000 x 10^9 = 10^12 mm^3 En bas: 10^6 mm^3 Ratio: 10^12 / 10^6 = 10^12-6 = 10^6 (1 million) Comparons en m^3 : Unités 1 mm^3 = 10^-9 m^3 En haut: 1000 m^3 = 10^3 m^3 En bas: 10^6 mm^3 = 10^6 x 10^-9 = 10^6-9 = 10^-3 m^3 Ratio: 10^3 / 10^-3 = 10^3-(-3) = 10^6 (1 million) Quelle est la logique?

Rappel

10^a x 10^b = 10^a+b

1 / 10^b = 10^-b

10^a / 10^b = 10^a-b

10^a = 10^a/2

ⁿ 10^a = 10^a/n

Voir Puissances

Théorie
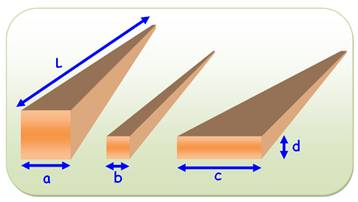
Ces trois objets ont une longueur L et une section différente. Les volumes sont respectivement: V = L x a x a V = L x b x b V = L x c x d De manière générique, si nous appelons S la surface (ou section) du volume V = L x S
Le volume d'un parallélépipède de longueur L est proportionnel à sa section S. Exemple En reprenant nos exemples, calculons le rapport entre un alignement de cube sur 1 km, les uns avec un côté de 1m et les autres avec un côté de 1 mm. Quel est le rapport entre les deux volumes? La longueur (L = 1km) est identique. Le rapport entre les volumes est comme le rapport entre les sections Pour l'un la section est de a x a = 1 m x 1 m = 1 m² Pour l'autre la section est de b x b = 1 mm x 1 mm = 1 mm² Le rapport entre les deux vaut : Ce qui est bien le résultat que nous avions trouvé.

APPLICATION: Nucléons dans l'Univers
L'univers comporte 10^80 nucléons dont le diamètre est de 1 fermi = 10^-15 m (moyenne). Quelle est la longueur d'une rangée formée par tous ces nucléons mis à la queue leu-leu? Quelle est la taille du carré formé par l'empilement de ces nucléons? Longueur L = 1 fermi x 10^80 = 10^80 fermis = 10^80 x 10^-15 = 10^65 m Sachant qu'une année-lumière (al) mesure 10^16 m; ou10^16 x 10^15 = 10^31 fermis. L = 10^65 / 10^16 al = 10^65-16 = 10^49 al
Volume (chaque nucléon est assimilé à un cube) V = L x S avec L = 10^80fermis et S = 1 fermi x 1 fermi = 10^80 x 1 x 1 en fermis-cube Sachant que 1 m = 10^15 fermis; Alors: 1 m^3= (10^15)^3 = 10^45 fermis-cube V = 10^80 / 10^45 = 10^35 m^3 C est tel que V = C^3 ou C = V C = (10^35) = (100 x 10^33) = (100) x 10^11 = 4,64 10^11 m À titre comparatif: distance Terre-Soleil: 150 millions de km = 1,5 x 10^2 x 10^6 x 10^3 = 1,5 10^11 m Empilés les nucléons de tout l'Univers formeraient un cube dont le côté serait trois fois la distance Terre-Soleil. Note: On empile les sphères comme des cubes et non en empilement optimal des sphères.

Piège! Raisonnement trop direct

Longueur totale des nucléons alignés: 10^65 m Pour mettre en cube, je prends la racine cubique: (10^65) = (100 x 10^63) =(100) x 10^21 = 4,64, 10^21 Raisonnement faux. La longueur ne suffit pas. Il faut prendre en compte le volume. Nous avons omis de prendre en compte la taille des nucléons, leur section. Raisonnement correct: Volume = 10^65 m x 1 fermi x 1 fermi 10^65 x 10^-15 x 10^-15 = 10^35 m^3 Vous avez compris que toute l'entrée en matière était un apprentissage pour éviter ce genre de blague dans les calculs de volume.

---

Suite	Volume du tétraèdre
Voir	Cube Géométrie – Bases Géométrie – Index Nucléons dans l'Univers Puissances de dix Unités de volume Univers