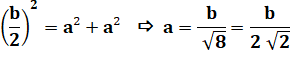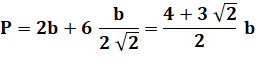NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Base de la Géométrie
Débutants Général Diaporama Junior	Mesures			Glossaire Périmètre
INDEX BASES GÉOMÉTRIE	Droite / Ligne	Périmètre	Surface / Aire
	Égalités	Distance	Unités
		Formulaire: Périmètres, aires et volumes
	et +	Sommaire de cette page >>> La croix >>> Le cube >>> Rectangle divisé en neuf rectangles >>> Papier plié et son périmètre >>> Cocottes >>> Exercices

PÉRIMÈTRE – Curiosités

Longueur de la circonférence d'une figure plane. Parfois amusant et déroutant de faire le tour de la question.

Voir la page principale sur le périmètre >>>

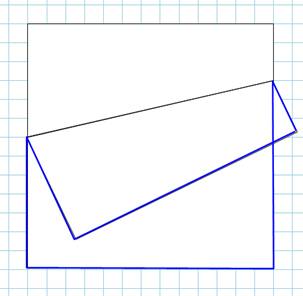
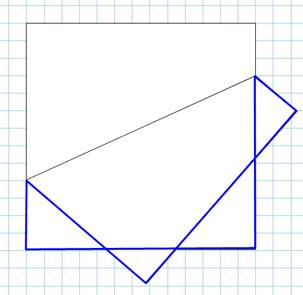
Énigme qui affole Internet: quel est le périmètre de ces deux figures ? >>>

Autre énigme: connaissant P trouver la valeur de a >>>

Voir Jeux et énigmes

La croix
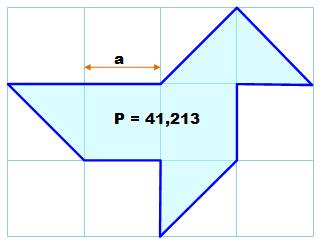
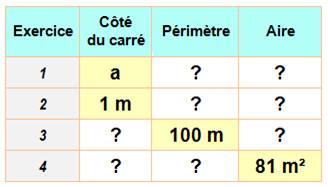
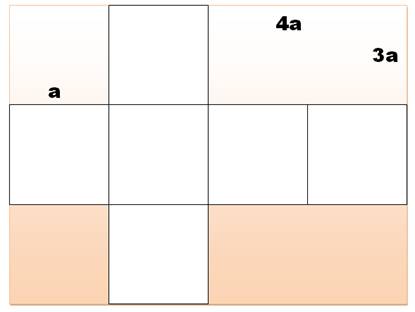
Quelques exercices avec cette croix comprenant neuf carrés élémentaires dont le côté mesure a. Quatre exercices indépendants
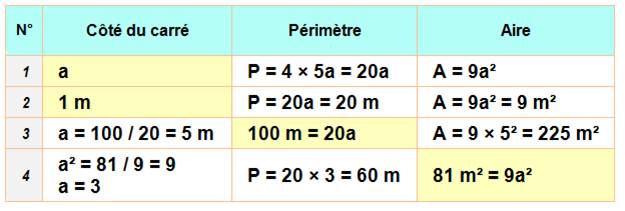
Solutions

Voir Déplacement sur la croix

Le cube
Quel est le périmètre de la feuille de carton nécessaire pour découper le patron de ce cube? Le patron du cube montre que la découpe nécessite un rectangle de 4a de long par 3a de large. Soit un périmètre de: P = 2 x (4a + 3a) = 14a Notez que c'est aussi le périmètre de la croix formant le patron. Normal, non ! Chaque côté externe des petits carrés peut être renvoyé sur le périmètre du rectangle.

Égalité

Quel le seul rectangle dont les côtés sont des nombres entiers et dont le périmètre est égal à l'aire.

C'est le carré de côté égal à 2, seul nombre tel que 2 + 2 = 2 x 2.

Voir Nombre 2 / Triangles de même aire et même périmètre

Rectangle divisé en neufs rectangles
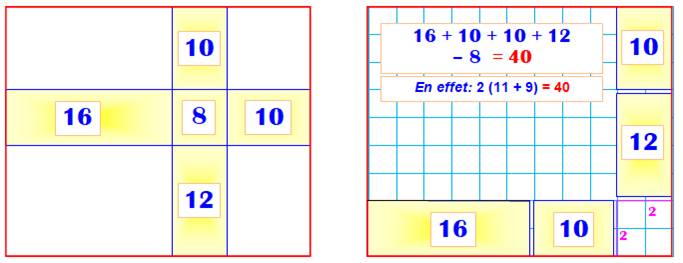
Énigme On donne la figure de gauche. Les nombres indiquent le périmètre des rectangles internes. Avec ces seules indications, retrouver le périmètre du grand rectangle.	Solution Plaquons les rectangles sur les bords comme sur la figure de droite. On observe que chaque côté des rectangles internes contribuent aux côtés du grand rectangle. Attention, les largeurs des bandes, contribuent 4 fois alors qu'on en a besoin que de 2. Deux fois ces segments représentent le périmètre du rectangle central. Il suffit alors d'ajouter le périmètre des rectangles internes et retrancher celui du rectangle central (ici un carré).
À retenir: le périmètre du GRAND rectangle est égal à la somme des périmètres des quatre rectangles périphériques, diminué du périmètre du rectangle cental.

Voir Brève n°411 / Autres énigmes sur périmètres et aires du rectangle divisé

Périmètre d'une feuille de papier pliée
Feuille de papier carrée. Son périmètre est la longueur de la ligne représentée en bleu. Nous nous proposons de suivre cette ligne bleue lorsque la feuille est pliée.
Le périmètre du carré prend cette forme de ligne brisée. Plions la feuille un peu plus loin …
La ligne brisée prend une forme encore plus tordue. Mais sa longueur est toujours celle du périmètre du carré.
Alors! Quel est le périmètre de l'ensemble de ces quatre triangles ?

Cocotte
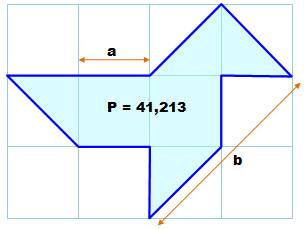
Problème Une cocotte est dessinée dans un quadrillage régulier de côté a. On connait le périmètre. Retrouvez la longueur du côté. Résolution Le truc consiste à introduire la longueur b. P = longueurs obliques + longueurs droites = 2 b + 6 a
La longueur b vaut deux fois la diagonale (théorème de Pythagore)
Avec le périmètre
Application numérique avec P = 41,213	b = 10 et a = 3,53…

Exercices
Problème Périmètre du terrain rectangulaire: 300m. Sa longueur dépasse sa largeur de 50 m. Quelle sont les dimensions du terrain? Explications Le périmètre est égal à deux fois la somme de la longueur (L) et de la largeur (l). La longueur L est égale à la largeur (l) + 50 mètres.	Résolution 2 (L + l) = 300 L + l = 150 L = l + 50 l + 50 + l = 150 2l + 50 – 50 = 150 – 50 2l = 100 l = 50 m L = l + 50 = 50 + 50 = 100m
Problème Une feuille de papier rectangulaire de dimensions A et B. Pliée en deux dans un sens, le périmètre est 48 cm; pliée en deux dans l'autre sens, il vaut 30 cm Taille de la feuille ? Explications Pour chaque pliage l'une des dimensions est divisée par 2. Attention, le périmètre n'est pas égal à la moitié du périmètre complet.	Mise en équations Périmètre pour le pliage 1: P1 = 2 (A/2 + B) = 48 cm Périmètre pour le pliage 2: P2 = 2 (A + B/2) = 30cm Système d'équations A + 2B = 48 2A + B = 30 Résolution (2 fois la 2 moins la 1) 3A + 0B = 60 – 48 = 12 A = 4 B = 30 – 2A = 22 Vérification P1 = 2 (2 + 22) = 48 P1 = 2 (4 + 11) = 30

Retour	Périmètre – Page principale
Suite	Papier plié Périmètre inconnu – Énigme (Brève 631) Transformation du boulanger Triangle orthocentrique Périmètre des figures classiques
Voir	Anamorphoses Fractales Géométrie – Index Géométrie – Vue d'ensemble Droites Format A4 … Triangles
Aussi	DicoMot DicoNombre Jeux, énigmes – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Bases/Perime.htm