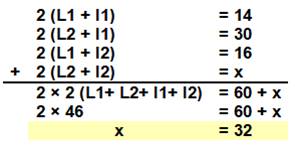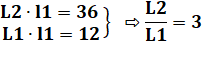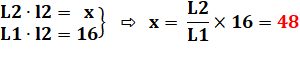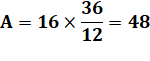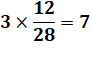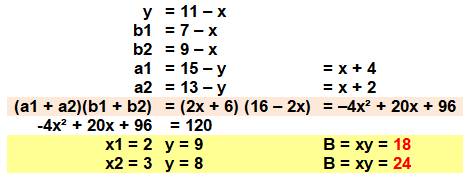|
Édition du: 28/01/2024 |
|
INDEX |
Géométrie – RECTANGLES |
||
![]()
|
RECTANGLE DIVISÉ en 4 ou en 9
Sur cette
figure, calculer l'aire du quatrième rectangle. Occasion de
résoudre une énigme difficile mêlant des données sur
les périmètres et l'aire. |
||
|
|
Sommaire de cette page >>> Périmètre du rectangle en 4 >>> Périmètre du rectangle en 9 >>> Périmètre des six briques >>> Aire du rectangle en 4 >>> Aire du rectangle en 16 >>> Énigme du périmètre et de l'aire |
Débutants Glossaire |
|
Problème On connait
le périmètre du grand rectangle (46) et ceux de trois rectangles (14, 30 et
16), calculez le périmètre du quatrième. Calcul
|
Rectangle
divisé en 4
Propriété La somme des périmètres de tous les rectangles internes est égale à
deux fois celui du grand rectangle.
|
|
|
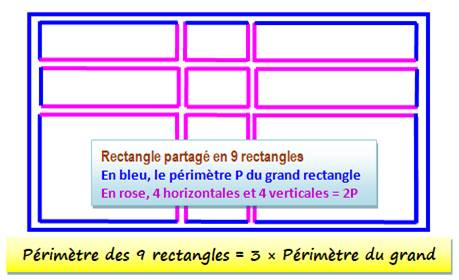
La somme
des périmètres des rectangles internes se déduit facilement avec un dessin du
type de celui proposé. Avec deux coupes verticales et deux horizontales,
on forme neuf rectangles. Les lignes de bordure épousent le périmètre du
grand rectangle. Alors que les quatre lignes horizontales et les quatre
lignes verticales reforment deux autres périmètres du grand. |
|
||
|
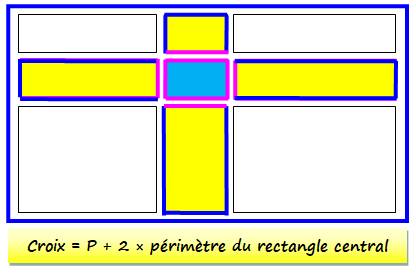
Croix Notez
cette configuration particulière en croix La somme des périmètres des rectangles jaunes est
égale au périmètre du grand rectangle (bleu) plus celui p du rectangle
central (rose) Autre formulation: CCENTRAL = PJAUNES – P |
|
||
|
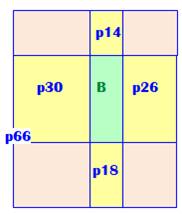
Énigme Avec les données de la figure, retrouvez le
périmètre B du rectangle interne vert. Solution En reprenant, la constatation précédente, on a : B = 30 + 14 + 26 + 18 – 66 = 88 – 66
= 22 |
|
||
Voir Rectangle divisé
en croix / Brève
411
|
Énigme Sachant
que le périmètre d'un seul rectangle est égal à 100, quel est le périmètre du
dessin ? Solution Lé périmètre de toutes les briques est égal à 6 x 100 = 600. Les traits en bleu ne font pas partie du
périmètre du dessin. On dénombre six longueurs de briques et six
largeurs couvrant donc trois périmètres, soit 300. Le périmètre du dessin est donc: 600 – 300 = 300. |
|
|
Voir Brève
560
![]()
|
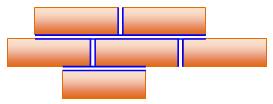
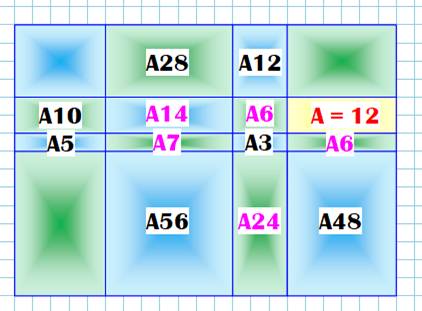
Problème On
connait les aires de trois des rectangles (12, 36 et 16), il faut calculer
l'aire du quatrième. Calcul
|
Rectangle
divisé en 4
Propriété L'aire du quatrième rectangle est la quatrième
proportionnelle des trois autres:
|
|
|
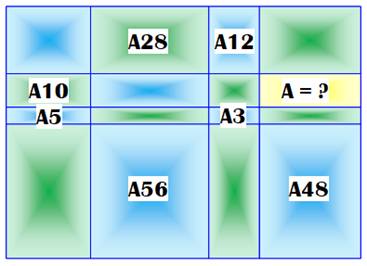
Problème On
connait les aires indiquées, il faut calculer l'aire du rectangle jaune. Calcul L'exemple précédent montre la marche à suivre: utiliser
la quatrième proportionnelle lorsque c'est possible. On isole par la pensée, quatre rectangles dont
trois sont connus et on calcule l'aire du quatrième. On procède de proche en
proche pour atteindre le rectangle désiré. Le premier calcul est le suivant,
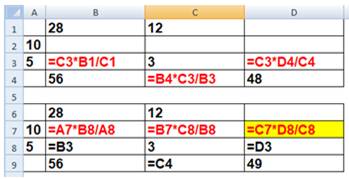
Suite avec tableur – formules (résultats
à droite)
|
Rectangle et données proposées
Deux tableaux de trois calculs
chacun
|
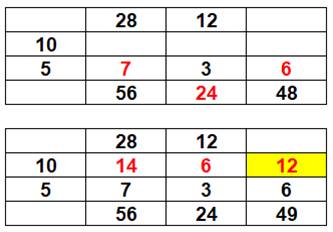
|
Résolution complète avec indication des dimensions
|
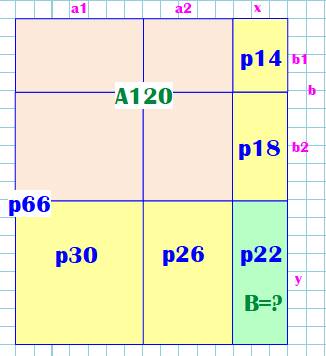
Énigme 1 Avec les données de la figure, retrouvez le
périmètre B du rectangle interne vert. Solution En reprenant, la constatation précédente, on a : B = 30 + 14 + 26 + 18 – 66 = 88 – 66
= 22 |
|
||
|
Énigme 2 (suite de la 1) On reprend
l'énigme précédente et on donne en plus l'aire des rectangles ocre: 120. Quel est
l'aire du rectangle B ? Illustration Pour favoriser la réflexion, on a translaté les
rectangles sur les bords. Le quadrillage est là pour vérification. Solution On établit le système d'équations qui montre que
les tailles des rectangles ne peuvent pas être quelconques. Pour le rectangle vert, de: 2x + 2y = 22, on
déduit que: y = 11 – x. Idem pour les
autres rectangles. L'aire de la zone ocre vaut 120 et s'exprime par
(a1+a2)(b1+b2) dans la quelle on remplace les valeurs par leur expressions en
fonction de x. On obtient une équation du second
degré qui produit deux solutions: 4x² – 20x + 24 =
0 Son discriminant vaut: 20² – 4 x 4 x
24 = 16 = 4² Et ses racines: x1 = (20 – 4) /
(2 x 4) = 2 x2 = (20 + 4) /
(2 x 4) = 3 |
C'est la seconde solution qui est représentée sur la figure. |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |