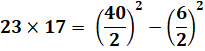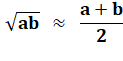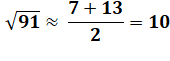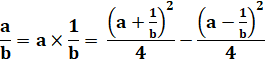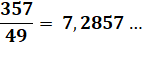|
Édition du: 23/09/2025 |
|
INDEX et autres pages sur la multiplication Techniques de calcul et calcul mental |
MULTIPLICATIONS |
||
|
Table 2, 5,
9 |
|||
|
Table 3, 4, 6, 7, 8 |
|||
|
Par
additions |
|||
|
Quatre quarts (ancien) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
MULTIPLICATION Méthode des quarts de carré Une méthode
calcul pratique avant l'avènement des calculatrices. Méthode qui nécessitait l'emploi
d'une table de valeurs numérique: le carré des nombres divisés par 4. |
||
|
|
Sommaire de cette page >>> Principe de calcul de la multiplication >>> Principe de calcul du carré >>> Principe de
calcul de la racine carré >>> Principe de calcul de la division >>> Historique >>> Table des quarts de carrés (1 à 50) >>> Une page de la table des quarts de carrés de
Blater |
Débutants Glossaire |
|
Identité remarquable La méthode des quarts de
carrés (quarter-square
method) est une technique de calcul qui permet de transformer une multiplication
en opérations plus simples : additions, soustractions et consultations
dans une table préétablie. Elle repose sur l’identité
remarquable indiquée. |
Identité
En développant
|
|
|
Application au produit Le produit de deux nombres a et b est égal au
quart de la différence de deux carrés. L'un est le carré de la somme des deux
nombres et l'autre, la différence. |
Identité utilisée pour la
multiplication
|
|
|
Multiplication simple Avec de petits nombres et des configurations qui
s'y prêtent bien, le calcul est très simple. Intérêt de la méthode Effectuer des multiplications sans poser la
multiplication elle-même. Que des additions et soustractions. Cette opération semble complexe, mais pour de
grands nombres, elle est plus efficace que la multiplication posée. |
Multiplication simple
|
|
|
Avec la table des quarts de carrés Nos anciens disposaient d'un livret d'une
centaine de pages listant tous les quarts de carrés comme celle de Joseph Blater. |
Multiplication élaborée
|
|
|
Méthode Ici, la méthode n’apporte pas de gain
particulier, mais la table des quarts de carrés contient déjà les valeurs
utiles. |
Identité applicable
|
|
|
Exemple Avec lecture directe dans la table des quarts de carrés. |
|
|
|
Méthode Cette approximation découle de la moyenne
arithmétique-géométrique. En combinant avec la méthode des quarts de carrés,
on peut estimer rapidement des racines carrées. |
Identité applicable Avec a =
b, on peut écrire:
|
|
|
Exemple Dans un premier temps, on cherche deux nombres
les plus proches possibles dont le produit est 91. La racine est proche de la moyenne de ces deux
nombres. |
Or la racine vaut 9,539… |
|
|
Méthode La division est en fait la multiplication d'un
nombre par l'inverse de l'autre. |
Identité applicable
|
|
|
Exemple La méthode nécessite l'empli d'une seconde table:
la tables des inverses (dite aussi: tables des réciproques). La méthode est laborieuse du fait de la présence
de grands et de petits nombres. |
Table: 1/49 ≈
0,0204
|
|
|
XVIIᵉ
siècle : |
|
|
XIXᵉ
siècle : |
|
|
1817 |
|
|
1887 |
|
|
XXᵉ
siècle : |
|
Table des quarts de carrés
(1 à 50)
|
n |
n²/4 |
n |
n²/4 |
n |
n²/4 |
n |
n²/4 |
|
1 |
0,25 |
14 |
49,00 |
27 |
182,25 |
40 |
400,00 |
|
2 |
1,00 |
15 |
56,25 |
28 |
196,00 |
41 |
420,25 |
|
3 |
2,25 |
16 |
64,00 |
29 |
210,25 |
42 |
441,00 |
|
4 |
4,00 |
17 |
72,25 |
30 |
225,00 |
43 |
462,25 |
|
5 |
6,25 |
18 |
81,00 |
31 |
240,25 |
44 |
484,00 |
|
6 |
9,00 |
19 |
90,25 |
32 |
256,00 |
45 |
506,25 |
|
7 |
12,25 |
20 |
100,00 |
33 |
272,25 |
46 |
529,00 |
|
8 |
16,00 |
21 |
110,25 |
34 |
289,00 |
47 |
552,25 |
|
9 |
20,25 |
22 |
121,00 |
35 |
306,25 |
48 |
576,00 |
|
10 |
25,00 |
23 |
132,25 |
36 |
324,00 |
49 |
600,25 |
|
11 |
30,25 |
24 |
144,00 |
37 |
342,25 |
50 |
625,00 |
|
12 |
36,00 |
25 |
156,25 |
38 |
361,00 |
||
|
13 |
42,25 |
26 |
169,00 |
39 |
380,25 |
Notez
qu'il s'agit en fait de la table de carrés des nombres avec un pas de 0,5.
Une page de la table des
quarts de carrés de Blater

Haut de page (ou double-clic)
![]()