NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/06/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	NOMBRES / FORMES
Débutants Types de Nombres	Produit contenant ses opérandes		Glossaire Nombres
INDEX Nombres en chiffres TYPES de nombres		Sommaire de cette page >>> Multiplications 10 x 10 >>> Multiplications 100 x 100 >>> Multiplications 1000 x 1000 >>> Multiplications 10 000 x 10 000 >>> Nombres dans leurs puissances >>> Produit de trois facteurs

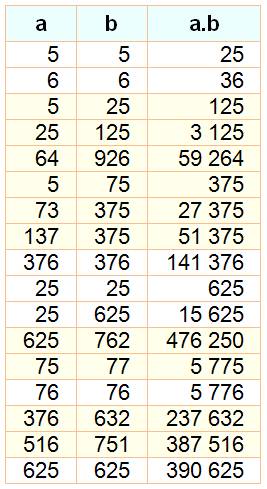
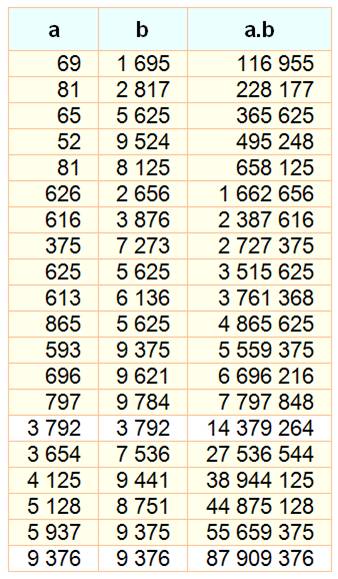
Produit contenant ses opérandes

Multiplication de a par b dont le produit contient les chiffres de a et b, ses facteurs.

Exemples: 75 x 77 = 5 775

64 x 926 = 59 264

Multiplications 10 x 10

Nous cherchons des multiplications a x b telle que le produit a.b contienne les chiffres de a et b dans l'ordre. Dans 64 x 926 = 59 264, le produit 59 264 contient les chiffres des deux opérandes. En effet: 59 264 et 59 264. Nous admettons les cas de superposition des chiffres. Remarque: Il existe une quantité de cas triviaux avec 0 tels que 100 x 61 = 6 100 et qui répondent aux critères (100 et 61 sont bien dans 6 100). Nous ignorons tous ces cas avec des zéros. C'est le cas aussi pour les multiplications par 1 telles que 1 x 81 = 81. Voyons les cas existants pour les multiplications jusqu'à 10 x 10. Seuls deux carrés émergent: 5 x 5 = 25 et 6 x 6 = 36

Multiplications 100 x 100
En explorant les multiplications jusqu'à 100 x 100, sept cas existent, dont trois seulement qui ne sont pas des carrés (en jaune). 5 5 25 6 6 36 5 25 125 5 75 375 25 25 625 75 77 5775 76 76 5776

Multiplications 1000 x 1000
En explorant les multiplications jusqu'à 1000 x 1000, sept cas existent, dont trois seulement qui ne sont pas des carrés (en jaune). Nous trouvons 17 cas dont les 7 trouvés pour 100 x 100. Dans cette panoplie sept sont des carrés avec les unités 5 et 6. Vous constatez que, pour tous ces cas, les chiffres des opérandes se chevauchent dans le produit.

Multiplications 10 000 x 10 000
Voici les 20 cas (dont deux carrés) en supplément de ceux présentés ci-dessus pour atteindre 10 000 x 10 000: Toujours pas, à ce niveau d'exploration, de cas de non-chevauchement des deux nombres dans le produit.

Nombre dans leurs puissances

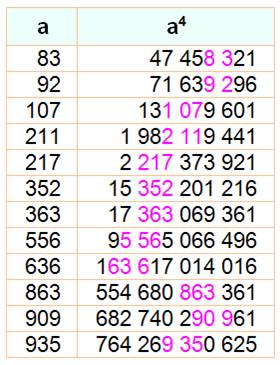
Vous avez noté dans le tableau ci-dessus que 3 792² = 14 379 264. Le nombre porté au carré est inclus dans son propre carré. Les suivants: 14 651² = 214 651 801 495 475² = 245 495 475 625 505 025² = 255 050 250 625 971 582² = 943 971 582 724 Ces cas sont rares. Par contre, le cas classique avec le nombre en fin du carré, est très courant. Voici un exemple: 109 376² = 11 963 109 376 Cas non triviaux avec des cubes: il y en a seulement 3 jusqu'à 1000^3. 32^3 = 32 768 56^3 = 175 616 782^3 = 478 211 768 Avec la puissance 4, il y a 12 cas jusqu'à 1000^4.

Produit de trois facteurs
Même exploration des produits contenants les chiffres de leurs trois facteurs pour chacun. On ne retient que les cas où les trois facteurs sont différents. Pour les facteurs jusqu'à 100, il y a 26 cas dont 9 pour lesquels le produit ne contient que les chiffres de ses facteurs.

Suite	Nombres dont les chiffres sont dans ses facteurs Multiplications Puissances et leurs unités Racines avec décimales identiques
Voir	Chiffres dans les nombres – Index Nombres à motif
DicoNombre	Nombre 64 Nombre 75 Nombre 625 Nombre 735 Nombre 3 792 Nombre 8 448
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/aaaIdent/MultiNb.htm