NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/05/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Opérations
Débutants Multiplications	Multiplications			Glossaire Opérations
INDEX CALCUL Nombre 9	Par 9	Par 10	Par 99
		Sommaire de cette page >>> Table de multiplication du 9 >>> Cas des grands nombres >>> Table de multiplication de 1 à 9 >>> Curiosités – Magie >>> Le 9 intercalé >>> Formation de repunits >>> Formation de repdigits

CURIOSITÉS ET AMUSEMENTS

Table de multiplication du 9

Voir Table complète

Apprentissage de la table

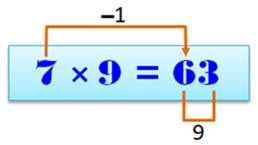
SIMPLE La table du 9 est la plus simple des tables non-banales. Allure générale: les dizaines vont en croissant, alors que les unités vont en décroissant. En pratique: 1) Faire –1 pour obtenir la dizaine: avec 6, on aura 5. 2) Prendre le complément à 9 pour avoir l'unité: avec le 5 trouvé, on ajoute 4 pour arriver à 9. Bilan: 6 × 9 = 54

Voir Comment apprendre les tables de multiplications

Table de multiplication par 9 et 9…9 pour n de 1 à 9 et plus

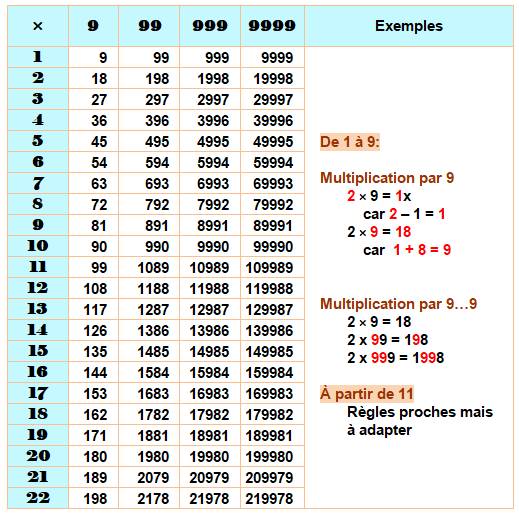
Multiplication et division mentales (deux chiffres)

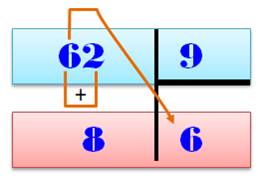
Multiplication de n par 9 Dizaine = n – 1 Unité = Complément à 9 de la dizaine	Division par 9 Quotient = dizaine Reste = somme des deux chiffres (tenir compte de la retenue éventuelle)

Voir autres explications en Division par 9, 19 … / Brève 559 / Brève 893

Division par 9 de grands nombres (calcul mental)

Multiplications rapides par 9 et 9…9

Il suffit de faire -1 et soustraire; le résultat tombe directement

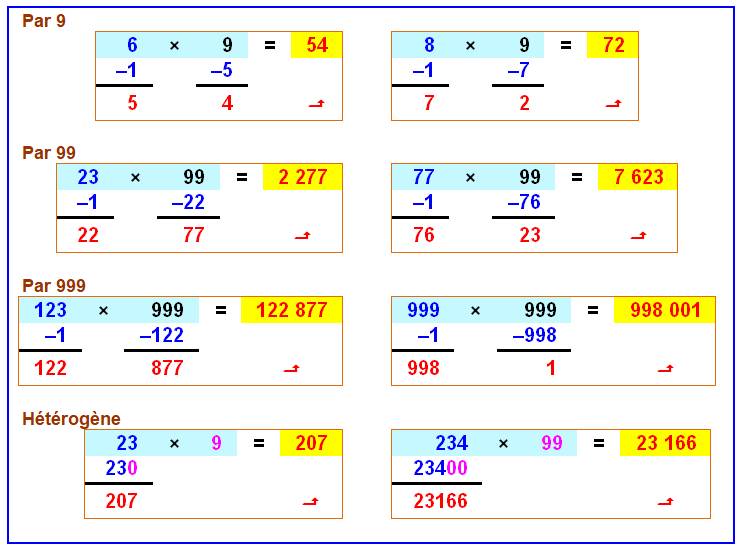
Voir Brève 500-994

CALCULS ET ASTUCES

Table de multiplication du 9
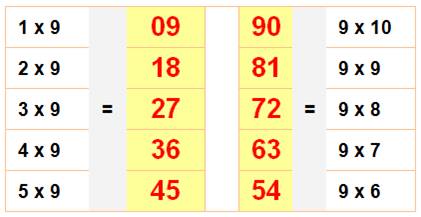
Élégante symétrie Qui facilite la mémorisation.
Notez cette disposition des chiffres du produit de n par 9: En haut les unités; En vertical les dizaines décalées d'un cran. Chiffre des dizaines = n – 1. Ex: (7 x 9 = 63). La somme des deux chiffres est toujours 9: Les unités vont décroissant; Les dizaines croissent.

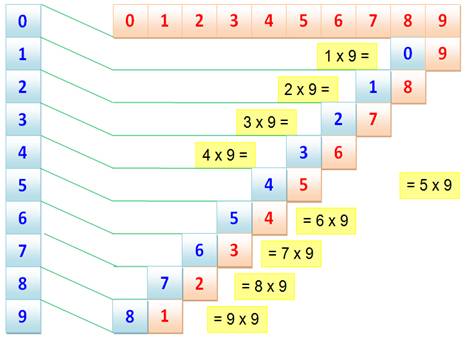
Voir Tables de multiplication y compris truc avec les doigts

Multiplication mentale par 9 des grands nombres
01234 x 9 = 11 106 08766	Multiplication rapide par 9 (méthode de Trachenberg). Prendre le complément à 9 de chaque chiffre, ou à 10 pour les extrémités.
12 340 08 766 21 106	Faire l'addition de ce complément avec le nombre x 10.
-1 11106	Retrancher 1 au chiffre de poids fort. Avec l'habitude, on calcule directement les chiffres les uns après les autres sans poser l'addition.

Table des multiplications de 1 à 9
Choisir deux chiffres en haut et suivre le chemin de rencontre vers le bas, seules les cases avec chiffres sont autorisés pour descendre à la case de croisement. Exemple: 3 x 7 3 => suivre: 3, 9, 12, 15, 18, 21 x 7 => suivre: 7, 49, 42, 35, 28, 21 => 21 est le résultat.

PREUVE PAR 9 ou Somme Numérique, ou Racine Numérique
La racine numérique est la somme des chiffres d'un nombre. La somme est répétée si nécessaire.	Le 9 est neutre dans la somme numérique. On l'élimine autant que possible. Il est remplacé par 0.	Soit une opération arithmétique. Son image avec les sommes numériques est également correcte. C'est la preuve par neuf.
456 4+5+6=15=>1+5= 6	45 6 9 + 6 => 6	123 x 456 = 56 088 6 x 6 = 36 => 9 9
123456789 => 10+10+10+10+5 = 45 => 4+5 = 9	123456789 => 18 27 36 45 9 => 0	15+12 +20 = 47 6 + 3 + 2 = 2 2

Voir Preuve – Glossaire / Modulo / Preuve par 11

Multiplication par 9 – Curiosités
Soit un nombre N.	87 594
Retourner les chiffres.	49 578
Soustraire (le plus petit du plus grand).	38 016
Racine numérique du résultat (somme de la preuve par 9).	R = 3 + 8 + 0 + 1 + 6 = 18 => 9
Quel que soit N.	R = 9
Autre exemple
Soit un nombre N.	87 594
La somme de ses chiffres.	8 + 7 + 5 + 9 + 4 = 33
La différence.	87 594 – 33 = 87 561
Sa racine numérique.	R = 8 + 7 + 5 + 6 + 1 = 9
Quel que soit N.	R = 9

Voir Suite >>>

LE 9 INTERCALE
1089 x 9 = 9801 Le produit par 9 retourne le nombre. 10 999 89 x 9 = 98 999 01 Intercaler des 9 conserve le motif. 2178 x 4 = 8712 Le produit par 4 retourne le nombre 21 999 78 x 4 = 87 999 12 Intercaler des 9 conserve le motif.

Formation de REPUNITS
0 x 9 + 1 = 1 1 x 9 + 2 = 11 12 x 9 + 3 = 111 123 x 9 + 4 = 1111 1234 x 9 + 5 = 11111 12345 x 9 + 6 = 111111 123456 x 9 + 7 = 1111111 1234567 x 9 + 8 = 11111111 12345678 x 9 + 9 = 111111111 123456789 x 9 + 10 = 1111111111

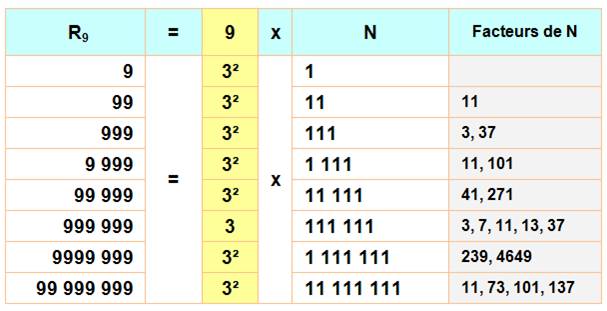
Voir RepUnit en 111 111

Formation de REPDIGITS
Multiplication Division Les résultats fractionnaires donnent (bien évidemment) des nombres cycliques (les décimales se répètent).

Suite	Multiplication Multiplication par 9, 99, 999 …
Voir	Calculs - Initiation – Index Kaprekar Multiplication Théorie des nombres
DicoNombre	Nombre 9
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/NeufMul.htm