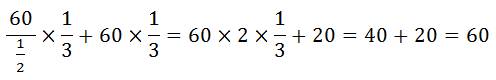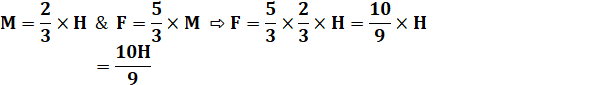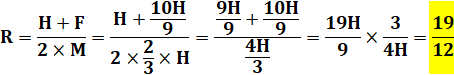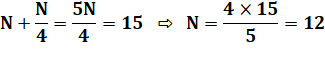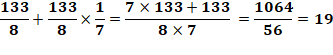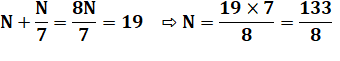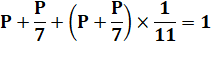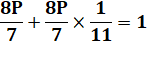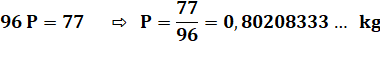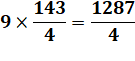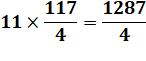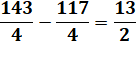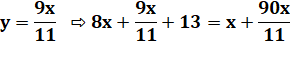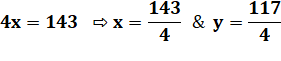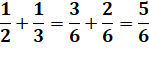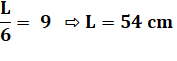|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FRACTIONS Exemples de calculs |
Voir Cours de 5e sur
les fractions
Amusement – Calculs ave 60
qui produit le nombre 60
|
|
|
Dans
cette communauté, 2/3 des hommes sont mariés et 3/5 des femmes sont mariées.
Quel est le rapport (la fraction) entre les personnes mariées et le total de
la population de cette communauté? |
|
Sept
cars pleins aux deux tiers partent de Sète. À Troyes, un quart des passagers
descend de chaque car. Peut-on mettre les trois quarts restant dans trois
cars ? |
|
|
||
|
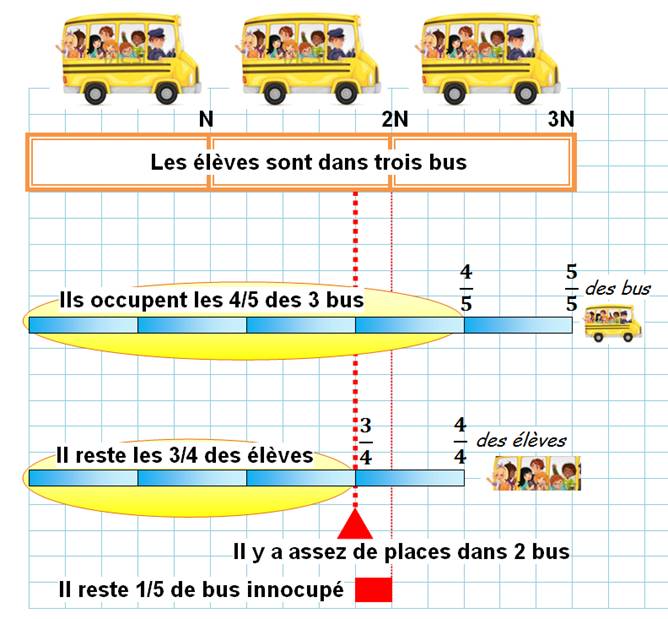
Des élèves occupent les quatre cinquièmes
de trois cars. Un quart des élèves descendent. Deux cars suffiront- t'ils pour transporter
les élèves restant? |
|
|
|
Choisissons N
comme étant la capacité d'un car (la quantité d'élèves maximum dans un car). |
Je
vous conseille de toujours faire un dessin, le plus réaliste possible pour
comprendre le problème et pour vérifier une fois les calculs faits. |
|
|
Illustration
Calculs
|
||
|
Problème Dans
cette communauté, 2/3 des hommes sont mariés et 3/5 des femmes sont mariées. Quel
est le rapport (la fraction) entre les personnes mariées et le total de la
population de cette communauté? Exploration Prenons
18 hommes, un nombre quelconque, divisible par 3. Ceux
qui sont mariés: 18 x 2/3 = 12. Il
y a autant de femmes mariées. Or, elles représentent les 3/5 des femmes. Il
y a donc 12 x 5/3 = 20 femmes. Le
rapport demandé: (18 hommes + 20 femmes) / (12 hommes mariés + 12 femmes
mariées) = (18 + 20) / (2 x 12) = 38 / 24 = 19 / 12. Solution générale Soit
H hommes, F femmes, et M mariés (hommes ou femmes).
Le
rapport demandé R:
Notez bien
que pour diviser par une fraction (4H/3), on multiplie par son inverse
(3/4H). >>> |
|
Problème (énoncé classique
présnt sur le Net) – Même type que celui traité ci-dessus Sept
cars pleins aux deux tiers partent de Sète.
À Troyes, un quart des passagers descend de chaque car. Peut-on mettre les
trois quarts restant dans trois cars ? Solution en chiffres Disons
qu’un car peut faire voyager 60 personnes, soit 180 pour 3 cars. Sept
cars au 2/3 : Bilan :
il reste 210 passagers que l’on ne peut pas loger dans trois cars à 180
places. Solution littérale qui
montre que la capacité (C) du car importe peu
|
|
|
||
|
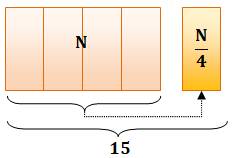
Problème Un nombre
augmenté de son quart donne 15. Quel est
ce nombre ? Papyrus Rhind Vérification La figure montre 5 parts pour 15. La part vaut 3. Le nombre cherché en compte 4, soit 4 x 3 = 12. |
Illustration
Résolution
|
|
|
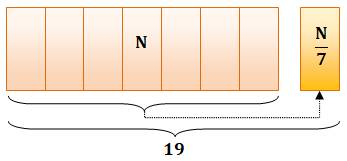
Problème Un nombre
augmenté de son septième donne 19. Quel est
ce nombre ? Papyrus Rhind Vérification
|
Illustration
Résolution
|
|
|
|
||
|
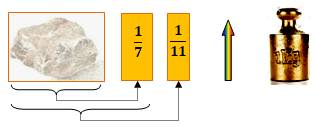
Problème À une
pierre, j'ai ajouté un septième de son poids puis un onzième du résultat. Le tout
pèse 1kg. Quel est
le poids de la pierre ? Tablette
babylonienne Vérification Q = P +
P/7 = 8P/7 = 0,916 R =
12Q/11 = 1,00 |
Illustration
Résolution
|
|
|
|
||
|
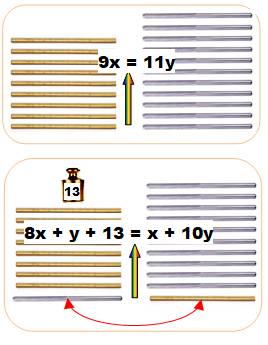
Problème On a 9
tiges d'or et 11 tiges d'argent qui, ensemble, ont le même poids. Si on intervertit
une tige or pour argent, les tiges en or sont plus légères de 13 grammes. Poids de
chaque tige ? Les neuf chapitres
sur l'art mathématique – Chine Vérification
Écart de poids: Cet écart est en plus à gauche pour la première
pesée. Il est en moins pour la seconde. Soit un bilan de 2 x 13/2 = 13. |
Illustration
Résolution
|
|
|
|
||
|
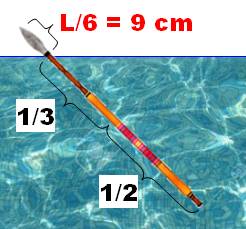
Problème Une lance
a la moitié et le tiers dans l'eau. Elle
dépasse de l'eau de 9 cm. Longueur
de la lance ? Problème médiéval
Vérification 1/2 L = 54 / 2 = 27 1/3 L = 54 / 3 = 18 Total immergé: 27 + 18 = 45 Reste émergé: 54 – 45 = 9 |
Illustration
Résolution La partie immergée compte pour: Soit 1/6 pour la partie émergée qui mesure 9 cm.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()