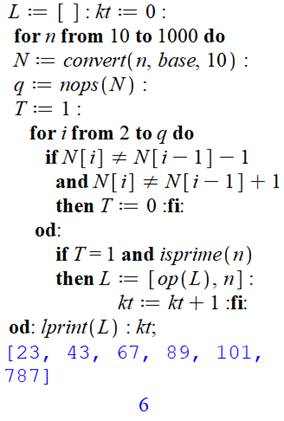|
|||||||||||||||||||||||||||||
![]()
|
|
|
|
|
|

|
|
||
|
|
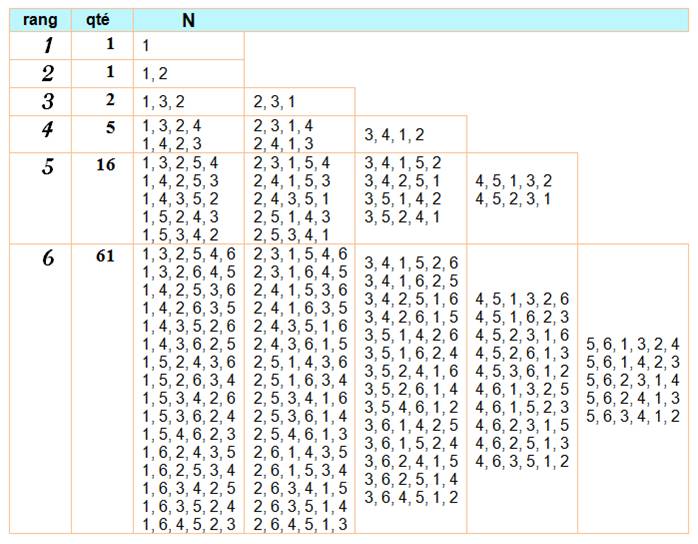
Utilisation
du package combinatoire de Mapple. n est la
quantité de rangs à explorer: tous les nombres de 1 à n
chiffres. N est une
table contenant toutes les permutations. M est la
quantité de permutations. Le
pointeur i explore toutes les M permutations T (test)
reste va rester vrai si le nombre est zigzag. Le
pointeur j examine les chiffres de chaque permutation. Si j est un
nombre pair (son modulo 2 est
nul) alors si son prédécesseur est plus petit, cette
permutation n'est pas zigzag (T= 0). Si j est
impair, même raisonnement. À
la fin de l'exploration d'une permutation, si T est resté égal
à 1, c'est que la permutation est bien zigzag. Elle est
imprimée sur l'écran. À
la fin des permutations de rang n, nous imprimons n et la quantité kt
de permutations zigzags, |
|
Voir Programmation
![]()
|
|
|||
|
Nombres dont deux chiffres voisins présentent une
différence de un. Ils sont 110 jusqu'à 10 000. |
10, 12, 21, 23, 32, 34, 43, 45, 54, 56, 65, 67, 76, 78, 87, 89, 98,
101, 121, 123, 210, 212, 232, 234, 321, 323, 343, 345, 432, 434, 454, 456,
543, 545, 565, 567, 654, 656, 676, 678, 765, 767, 787, 789, 876, 878, 898,
987, 989, 1010, 1012, 1210, 1212, 1232, 1234, 2101, 2121, 2123, 2321, 2323,
2343, 2345, 3210, 3212, 3232, 3234, 3432, 3434, 3454, 3456, 4321, 4323, 4343,
4345, 4543, 4545, 4565, 4567, 5432, 5434, 5454, 5456, 5654, 5656, 5676, 5678,
6543, 6545, 6565, 6567, 6765, 6767, 6787, 6789, 7654, 7656, 7676, 7678, 7876,
7878, 7898, 8765, 8767, 8787, 8789, 8987, 8989, 9876, 9878, 9898 |
||
|
Premiers oscillants. Ils sont 39 jusqu'à 1 000 000. Dont 4 ascendants purs (rouges) et 2 descendants purs (bleus). |
23, 43, 67,
89, 101, 787, 4567,
12101, 12323, 12343, 32321, 32323, 34543, 54323, 56543, 56767, 76543, 78787, 78989, 210101, 212123, 234323,
234343, 432121, 432323, 432343, 434323, 454543, 456767, 654323, 654343,
678767, 678989, 876787, 878789, 878987, 878989, 898787, 898987, De 1 000 000
à 5 000 000: 1012321, 1210123, 1212121, 1234543, 3210101, 3210121, 3212101,
3212123, 3212323, 3232321, 3432101, 3454343, 3456767… |
||
|
Programme de recherche
|
Commentaires Liste L qui recevra les nombres oscillants premiers. kt pour les compter. Boucle d'analyse des nombres jusqu'à 10000, par exemple. Conversion en décimal qui a pour effet d'isoler les chiffres.
Quantité de chiffres en q. T est un indicateur mis à 1 en imaginat
que n soit oscillant premier. Boucle d'analyse des chiffres de 1 à q. Si deux voisins ne sont
pas proches l'indicateur T est mis à 0. Si T est maintenu à 1 à la fin de l'analyse des
chiffres, alors c'est un candidat; reste à vérifier qu'il est premier.
Si oui, n est placé dans la liste L. On imprime la liste et le compteur. |
||
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre
|
|
|
Cette
page |
![]()