|
|||||||||||||||||||||||||||||||
![]()
|
Famille |
Nombre / Diviseurs / Multiplicatif / Premiers |
|
Approche |
5!
= 1 x 2 x 3 x 4 x 5 = 120 est divisible par au moins 2, 3, 4 ,5 En
fait les diviseurs de 120 sont 1 2 3 4
5 6 8 10 12 15 20 24 30 40 60 120.
5!
– 1 = 119 = 7 x 17: il n'est pas premier 5!
+ 1 = 121 = 11² : il n'est pas
premier 3!
– 1 = 5 : premier 3!
+ 1 = 7 : premier |
|
Définition |
Nombre premier f Nombre
premier en n!
– 1 ou n!
+ 1 |
|
Propriétés |
Considérons les nombres N = n!
+ m avec m < n m est nécessairement l'un des facteurs de n! et,
alors, n! = k.m Notre nombre N devient N
= k.m + m qui est divisible par m, N est un nombre composé, Sauf lorsque m = 1.
n! – n à n! + n
l n! – 1 ou n! + 1 Illustr
|
|
Anglais |
Prime of the form n! ± 1 |
|
|
|
|
|
|
Plages
des nombres de n! – n à n! + n pour n de 2 à 6. En rouge les
nombres premiers
On
note les exceptions pour n = 2 (2! = 2 est premier) et pour 3 (3! – 3 = 3 est
premier). Plage de nombres
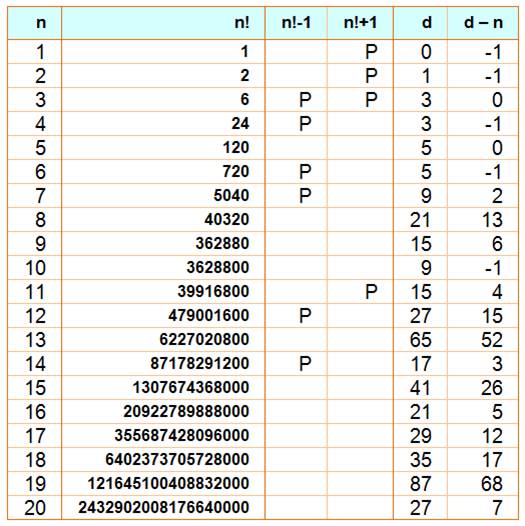
composés derrière une factorielle Ce
tableau donne la quantité d de
nombres composés qui suivent
le nombre n! + 1. Il est toujours égal ou plus grand que n – 1. L'excédent d
– n tend à croître avec n, mais souffre d'exceptions, comme avec 20!
|
|
Voir Primorielles
|
|
|||||||||||||||||||||
|
Nombres
premiers factoriels
Nombres
premiers f et
génér pour n jusqu'à 100
|
|||||||||||||||||||||
|
N = n! + n + 1
est premier pour n = {2, 4, 6, 10, 52} n jusqu'à 1000. N = n! + 1 est
premier pour n = { 2, 3, 11, 27, 37, 41, 73, 77,
116,
154, 320, 340, 399, 427} n jusqu'à 500. |
|
|
||
|
|
Commentaire Boucle de formation des factorielles avec n égal le précédent
multiplié par les nombres successifs. Formation de deux listes si n! + 1 est premier et si n! – 1 est
premier. Impression des deux listes en fin de traitement. |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremFact.htm |
![]()