|
Édition du: 19/10/2020 |
|
INDEX |
Types de Nombres – Polynômes |
|
|
Cunningham – Généralisés |
Cunningham – Simples |
|
![]()
|
Cunningham simples Nombres
binomiaux (deux termes) égaux à une puissance
plus ou moins 1. Ils peuvent être
généralisés en somme ou différence de deux
puissances. Ils peuvent être
particularisés en nombres
de Mersenne ou nombres de
Fermat. |
||
|
|
Sommaire de cette page >>> Approche >>> Définition et notation >>> Liste >>> Statistiques >>> Exemples de factorisation |
Débutants Glossaire |
|
Mathématicien
britannique né à Dehli (Inde). Archéologue,
militaire puis mathématicien expert en théorie des nombres. Notamment:
recherche des facteurs des grands nombres de la forme: Le
projet Cunningham, commencé en 1925 avec Woodall est toujours d'actualité. Il
vise à recenser la décomposition en facteurs premiers des nombres de
Cunningham pour b = 2, 3, 5, 6, 7, 10, 11, 12 et n très grand. |
Voir Contemporains
|
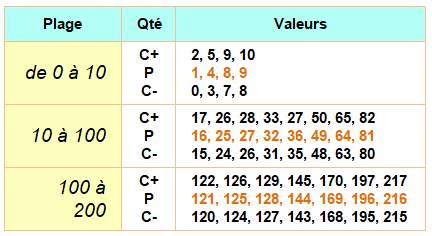
Nombre de Cunningham Nombre égal à une puissance pure
plus ou moins 1. Tableau Le tableau indique les nombres puissances en
marron et les nombres de Cunningham associé sur les lignes en haut (sur-Cunningham
ou C+) et en bas (sous-Cunningham ou C-). |
|
|
|
Les nombres de Cunningham (simples) sont du type
binomial (somme algébrique de deux termes) dont le second terme est 1. Les nombres b et n sont des nombres entiers
positifs, avec n > 1. |
|
|
|
Goldbach a montré que la somme des inverses des
"sous-puissances" tend vers 1. La somme des inverses des nombres listés
ci-dessous (de 3 à 1727) est égale à 0,9714116313. La somme pour les inverses des C+ atteint: 1,26… |
|
|
|
Intérêt: rechercher les nombres de Cunningham qui
sont premiers
et, sinon, leur factorisation. Les Cunningham premiers sont rares. |
Cas des nombres de Mersenne qui détiennent le record des plus grands nombres
premiers connus. |
|
|
Tous les C- sont composés
sauf éventuellement si b = 2 Si l'exposant est composé, il est également divisible.
|
bn – 1 est divisible
par b – 1 (b>2) bn.m – 1 est divisible
par bm – 1 |
|
|
Pour que 2n – 1 soit premier |
n doit être premier. |
|
|
Tous les C+ avec b impair sont divisibles par 2 La puissance d'un nombre impair est impaire. |
(2k + 1)n + 1 est divisible par 2 |
Factorisation de 2k +1 à la puissance n et mise en évidence du facteur 2

|
Les C+ en 2n + 1 sont divisibles
par 3 lorsque n est impair. |
22k+1 + 1 est divisible
par 3 Ex: 23 + 1 = 9 = 3 x 3 25 + 1 = 33 =
3 x 11 |
|
Tous les C+ avec exposant impair sont divisibles |
b2k+1 + 1 est divisible
par b + 1 Ex: 77 + 1 = 823 543 = 8 x 102 943 |
|
Tous ces C+ avec n pair (n = 2h.k)
sont divisibles |
b2^h.q + 1 est divisible
par b2^h + 1 |
|
Conséquence des énoncés ci-dessus: Condition nécessaire, mais non suffisante, pour
que les C+ soient premiers: n = 2m |
Ce sont les nombres de Fermat. |
|
Nombres de Cunningham connus |
Jusqu'à 98 chiffres et n jusqu'à 58. |
|
Nombre C- 3, 7, 8, 15, 24, 26, 31,
35, 48, 63, 80, 99, 120, 124, 127, 143, 168,
195, 215, 224, 242, 255, 288, 323, 342, 360, 399, 440, 483, 511, 528, 575, 624,
675, 728, 783, 840, 899, 960, 999, 1023, 1088, 1155, 1224, 1295, 1330, 1368,
1443, 1520, 1599, 1680, 1727, … Les seuls premiers (en rouge) sont les nombres de
Mersenne. |
Nombres C+ 2, 5, 9, 10, 17, 26,
28, 33, 37, 50, 65, 82, 101, 122, 126, 129, 145, 170, 197, 217, 226, 244, 257,
290, 325, 344, 362, 401, 442, 485, 513, 530, 577, 626, 677, 730,
785, 842, 901, 962, 1001, 1025, 1090, 1157, 1226, 1297,
1332, 1370, 1445, 1522, 1601, 1682, 1729 Cette suite est égale à celle de gauche plus deux
unités. |
|
|
122
puissances pures (1,22%) 363
puissances pures et Cunningham (3,63 %) 9637
non puissance pure et non Cunningham (96,37%) Les
"non" jusqu'à 100: 6, 11, 12, 13, 14, 18, 19, 20, 21, 22,
23, 29, 30, 34, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 51, 52, 53, 54, 55, 56,
57, 58, 59, 60, 61, 62, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79,
83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100. |
Exemples
de factorisation des nombres 2n + 1 pour
n de 100 à 110
n, C+, f (annonçant la factorisation),
facteurs

Situation actuelle
|
Les nombres de
Cunningham factorisés jusqu'à: 21300
, 3850 , 5550 , 6500 , 7450 , 1040 , 11350 , 12350 |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |