NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/05/2021 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Chiffres
Débutants Nombres	Chiffres et opérations			Glossaire Chiffres
INDEX Somme-Produit Ch Narcissiques Formes et motifs Nombres en chiffres Chiffres Types de nombres Jeux et énigmes	Sommes des chiffres		Produit des chiffres	Énigme 711
	Somme + Produit		Somme ds Produit
		Sommaire de cette page >>> Énigme 711 >>> Type de problème du même genre >>> Avec deux réels >>> Avec trois réels >>> Avec quatre réels >>> Avec S = P = R imposé >>> Solution de l'énigme 711 >>> Programmation du Pb 711 >>> Raisonnement arithmétique

>>> Énigme du 711: somme de nombres = leur produit

Nombres

SOMME = PRODUIT

Fameuse énigme de la caissière qui multiplie au lieu d'ajouter et pourtant elle encaisse la somme juste.

Résolution de cette énigme par raisonnement et par programmation. Exploration des cas similaires pour constater qu'ils sont finalement assez nombreux.

Énigme 711
Un Américain rentre dans un magasin Seven-Eleven (7-11) et fait ses courses. À la caisse, sa facture s'élève à 7,11 dollars pour quatre articles, mais il a constaté que la caissière avait frappé sur la touche "multiplier". Sans sourciller, la caissière reprend le décompte et lui présente la nouvelle facture: 7,11dollars. Quel est le prix de chacun des quatre articles?

Solution >>>

Exploration

Divers types de problèmes du genre
Nombres entiers avec ou sans répétitions	Somme des chiffres = somme de leur produit = N Il existe une solution pour tout N, mais rarement plus d'une.	1 + 2 + 3 = 1 x 2 x 3 = 6 1 + 1 + 2 + 4 = 1 x 1 x 2 x 4 = 8		>>>
Avec des nombres entiers	Aucune solution, sauf en chiffres (ci-dessus)
Avec des nombres réels	Une infinité de solution	Exemples ci-dessous		>>>
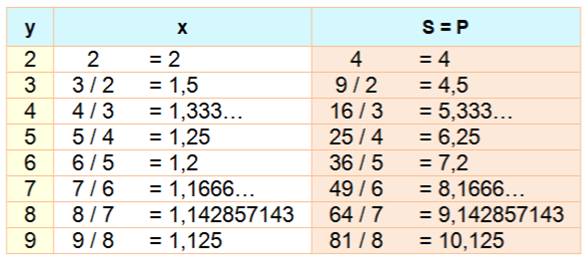
2 nombres	Un nombre est choisi, le second est calculé.	11 + 1,1 = 11 x 1,1 = 12,1		>>>
3 nombres	Deux nombres sont choisis, le troisième est calculé.	1 + 2 + 3 = 1 x 2 x 3 = 6 1 + 4 + 5/3 = 1 x 4 x 5/3 = 20/3		>>>
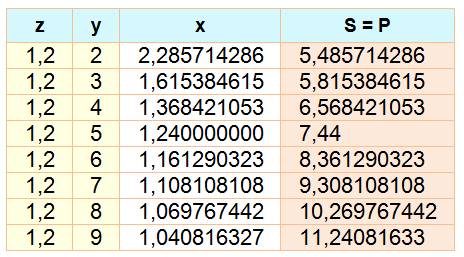
4 nombres	Trois nombres sont choisis, le quatrième est calculé.	1 + 2 + 3 + 1,2 = 1 x 2 x 3 x 1,2 = 7,2		>>>
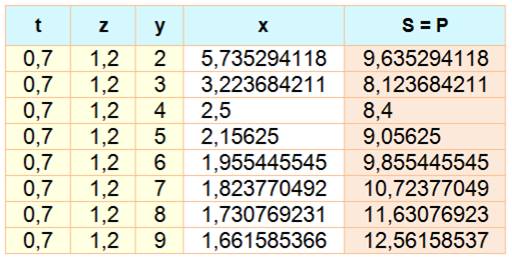
Idem sous contrainte de valeur de R	Comment calculer ?	Problème 711		>>>

Sr = Pr = R avec DEUX nombres réels
Avec deux nombres. La valeur de y étant choisie, x est calculé.	x = y / (y – 1).
Exemples Voir Résolution d'une équation du deuxième degré en S et P

Sr = Pr = R avec TROIS nombres
Avec trois nombres. L'indice de S et de P indique la somme et le produit sur trois nombres Deux nombres sont choisis, le troisième est calculé.	x = (y + z) / (yz – 1). x = S2 / (P2 – 1)
Exemples

avec QUATRE nombres
Avec quatre nombres. Trois nombres sont choisis, le quatrième est calculé.	x = (y + z + t) / (yzt – 1). x = S3 / (P3 – 1)
Exemples

Avec R imposé
Avec deux nombres La valeur de R impose la valeur de y solution d'une équation du deuxième degré. Attention: pas de solution pour toute valeur de R.	x + y = xy = R x = R/y R/y + y = R y² + R = Ry y² – Ry + R = 0
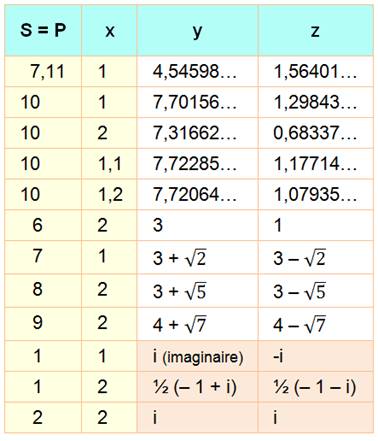
Exemples R = 4 y = 2 x = 2 R = 4,5 y = 1,5 x = 3 R = 7,11 y = 5,90617… x = 1,20382… R = 7,2 y = 6 x = 1,2

Avec trois nombres Nous avons deux équations seulement pour trois inconnues. On conserve x comme variable. Il y a donc une infinité de solutions pour toutes les valeurs de x qui "marchent".	x + y + z = xyz = R Avec y + z = S et yz = P x + S = xP = R P et S en fonction de R et x P = R/x S = R – x y et z sont les racines de y² – Sy + P = 0
Exemples

Avec quatre nombres Nous avons deux équations seulement pour quatre inconnues. x et y seront les variables et on pose X = x + y et Y = xy Nous voilà revenus au cas précédent avec un choix pour x et y. La solution n'existe pas toujours. Les solutions sont extrêmement rarement des valeurs à deux décimales comme dans la solution du problème 711.	x + y + z + t = xyzt = R X + S = YP = R P et S en fonction de R et X P = R/Y S = R – X y et z sont les racines de y² – Sy + P = 0
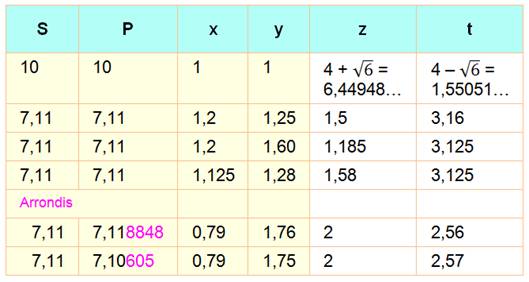
Exemples avec solutions à deux ou trois décimales; et possibilité d'arrondir le résultat de la multiplication.

Résolution de l'énigme

Énigme 711 - Solution

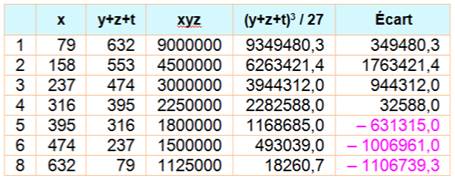
1,20 + 1,25 + 1,50 + 3,16 = 1,20 x 1,25 x 1,50 x 3,16 = 7,11 Comme indiqué ci-dessus, la solution n'est pas évidente à trouver. Il faut avoir le flair d'estimer x et y. Pour y arriver on peut programmer une recherche ou alors tenter un raisonnement arithmétique. Dans tous les cas, plusieurs remarques sont exploitées: Passage à des nombres entiers (des dollars aux cents) pour ne faire des opérations que sur des nombres entiers. Alors: Som = 711 et Pd = 711 000 000. Chacun des quatre nombres (x, y, z et t) doit diviser Pd. Facteurs de 711 000 000 = 2^6 x 3^2 x 5^6 x 79. Valeurs de x, y z et t interchangeables (commutativité).

Retour / Calcul

Programmation (Mapple)
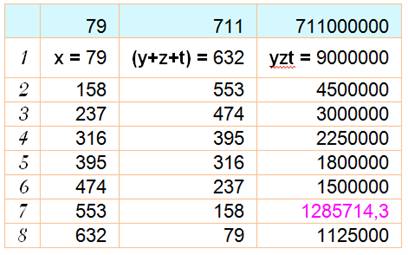
120, 125, 150, 316, 711, 711000000	Réinitialisation. Somme et produit demandés. Balayage en x de 1 à 711. Examen de x que si x divise le produit. Même chose en y, z et t. Le balayage commence à la valeur de la variable précédente. Inutile de refaire avec y les valeurs déjà vues pour x. Les quatre valeurs sont interchangeables. Le balayage pourrait être arrêté à 708 = 711-4, car trois valeurs sont au moins égales à 1. Calcul de la somme et du produit de ces quatre valeurs courantes. Si elles satisfont nos conditions, alors les imprimer. Fin des conditions (en if) et des boucles (en do). L'exécution ne dure que quelques secondes. Sans les tests de divisibilité, ce serait plutôt une heure. Valeurs trouvées par le programme, y compris somme et produit pour vérification.
Ce programme permet de trouver les valeurs dans ce cas précis. En ajustant la première ligne, il s'applique à toutes autres valeurs. On peut chercher à accélérer encore le programme, par exemple, en ne traitant que les diviseurs de Pd. Pour être tout à fait général (trouver et lister les diviseurs de Pd), le programme est d'un niveau un peu plus complexe.

Voir Programmation

Raisonnement arithmétique
L'exploration est assez longue. En voici l'explication pas à pas. Le produit est divisible par 79. Le premier nombre x est inférieur à 711. Strictement, car les trois autres articles coûtent au moins 1 cent. Énoncé des multiples de 79. Puis, déduction immédiate de la somme et du produit des trois autres. Le 7^e multiple, produisant un quotient à virgule est à rejeter (7 n'est pas un diviseur du produit).	Un seul des nombres est divisible par 79. Disons x. x = 79 k < 711
Une propriété des progressions arithmétiques et géométriques permet d'éliminer trois cas. Comparons ces valeurs dans nos sept cas. Trois valeurs négatives en ligne 5, 6 et 8, autant de cas à éliminer. Nous avons réduit notre problème à l'examen de quatre cas seulement.

Notons qu'aucun des x restants n'est divisible par 5. Alors yzt est divisible par 5^6. Seule la somme en ligne 4 est divisible par 5. Ignorons cette ligne pour le moment.	(y, z , t) = {5, 5^2 = 25, 5^3 = 125, 5^4 = 625} Chacun ne pouvant pas dépasser 5^4 pour rester inférieur à 711.
Lignes 1, 2 et 3. Avec la remarque précédente. C'est donc le produit zt à lui seul qui doit être divisible par 5^6.	La somme (y + z + t) n'est pas divisible par 5. Un des nombres au moins n'est pas divisible par 5. Disons y. (z, t) = {5, 5^2 = 25, 5^3 = 125, 5^4 = 625} Si z = 5^4 = 625, alors t = 5^2 = 25 y + 625 + 25 = y + 650 Valeur supérieure aux sommes des lignes 1, 2 et 3. Donc, mauvais choix pour z. Seule possibilité: z = 5^3k = 125k et t = 5^3k' = 125k'. k et k' sont inférieurs à 5 (et pas 5, cf. ci-dessus) (z, t) = {125, 250, 375, 500}
Résumons, hors la ligne 4 qui restera à être examinées séparément. Peut-on atteindre notre somme et notre produit avec ces valeurs?	Pd = 711 000 000 = 2^6 x 3^2 x 5^6 x 79. x = 79 2^i 3^j y = 2^i' 3^j' z = 125 2^i'' 3^j'' t = 125 2^i''' 3^j'''
Seules trois possibilités pour z et pour t. En vertu de la somme des deux, inférieure à 711. Ce qui permet de reconstituer le produit.	z et t < 632 =>125 x 2 = 250; 125 x 4 = 500; 125 x 3 = 375. z = t = 250 (toute autre somme dépasse 632; cas de 250 + 375 + 5 = 630, cependant, les facteurs 2 et 3 ne sont pas encore pris en compte et avec un simple x2 sur le 5, la somme est trop grande). Pd = (79 x 2^i x 3^j) x (2^i' x 3^j') x (125 x 2) x (125 x 2) = 2^i+i'+2 x 3^j+j' x 5^6 x 79 Som = x + y + 500 = 711 => x + y = 271
Valeurs possibles des x (selon les trois premières lignes du tableau) et comparaison à la somme. Est-ce que produit convient? Non, les lignes 1, 2, 3 du tableau sont à éliminer	x = {79, 158, 237} y = 271 – x = {429, 113, 34} P = 79 x 429 x 250² => Non P = 158 x 113 x 250² => Non P = 237 x 34 x 250² => Non

Notre seul espoir: la ligne 4 avec x = 316. Attention, cette fois la somme est divisible par 5: les trois termes sont divisibles par 5. Cependant la somme n'est pas divisible par 25: par de carré de 5 dans chacun des termes.	x = 2^2 x79 y = a 5^k z = b 5^k' t = c 5^k'' avec k + k' + k'' = 6 et k, k', k" 0, 2. On peut avoir, pour chacun des termes: 5, 5 , 5^4, mais 5^4 = 625, trop grand pour 395. 5, 5^2, 5^3 configuration qui peut convenir.
La valeur de t ne doit pas dépasser la somme 395: ce qui ne laisse que trois valeurs pour t. Le cas t = 375 laisse seulement 20 = z + t, or cette somme vaut au moins 25 + 5 = 30. Même remarque pour z = 300 qui avec t = 125 dépasse la somme autorisée	x = 2^2 x79 y = 2^i 3^j 5 z = 2^i' 3^j' 5^2= {25, 50, 100, 150, 200, 300} t = 2^i'' 3^j'' 5^3 = {125, 250, 375} avec y + z + t < 395
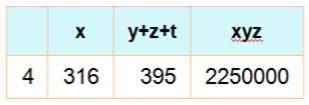
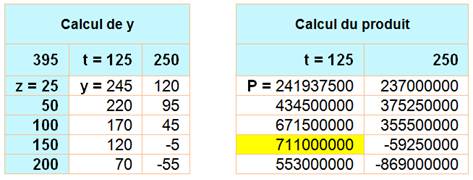
La quantité de cas à examiner n'est plus importante. nous pouvons nous permettre de les examiner une par une. De la somme 395, nous déduisons la valeur de y Disposant des quatre valeurs, ne reste plus qu'à tester le produit.	BINGO! x = 316, y = 120, z = 150 et t = 125

Bilan

Cette énigme est très facile à résoudre par programmation. Plus laborieuse par raisonnement. Trouver d'autres cas où les valeurs fonctionnent aussi bien nécessite une exploration par programme. Il y en a beaucoup …

Voir Table

Merci à Roger Fourneaux pour l'idée de cette page

Calculs inspirés par le site cité ci-dessous

Suite	Table de nombres de même configuration que 711 Somme et produit de chiffres – Identiques Somme-Produit des chiffres – Index
Voir	Addition Allumettes et nombres Bases de numération Chiffres à barre – Comparaison Chiffres en lettres Nombres à barres en lettres Nombres en toutes lettres Numération - historique Pannumérique Unité des puissances
DicoNombre	Nombre 711 Nombre 7,11
Site	The 7-11 Problem par Joshua E. Hill (2011). Programmation et solution complètes.
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Pb711.htm