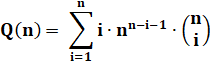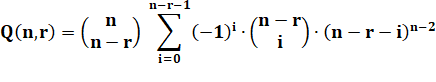Arbres étiquetés

Types d'arbres dont tous les nœuds sont numérotés. Ils obéissent à certaines règles de numérotation. Certaines configurations avec les mêmes feuilles sont redondantes et donc ignorées.

Sommaire de cette page

>>> Les trois arbres étiquetés d'ordre 3

>>> Les seize arbres étiquetés d'ordre 4

>>> Les 125 arbres étiquetés d'ordre 5

>>> Arbres étiquetés – Formule de Cayley

>>> Arthur Cayley – Biographie

>>> English corner

Débutants

Dénombrement

Glossaire

Combinatoire

Anglais : Labeled tree

Voir Autre variété d'arbres de Cayley

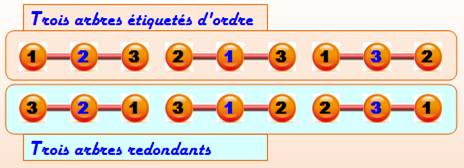
Les trois arbres étiquetés d'ordre 3		haut
Exemple avec trois sommets Avec les arbres numérotés à trois sommets (n = 3 ou ordre 3), les numéros des extrémités sont interchangeables. Seul le numéro central est original. Soit trois possibilités (1, 2 ou 3). Il existe seulement trois arbres étiqueté d'ordre 3. Trois autres, en inversant les extrémités sont redondants.
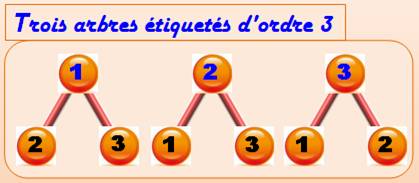
Présentation classique avec le nœud (sommet) racine en tête, en haut. Seul le nœud-racine définit un arbre éligible. Les sommets-feuilles sont permutables. Note: habitude prise de mettre la "racine" en haut, contrairement à la nature !	L'échange entre les deux feuilles produit des arbres semblables Dit-autrement, les feuilles sont communtatives.

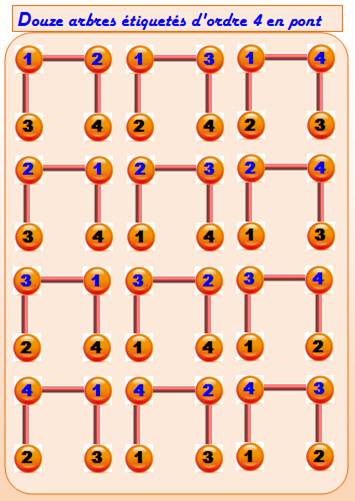
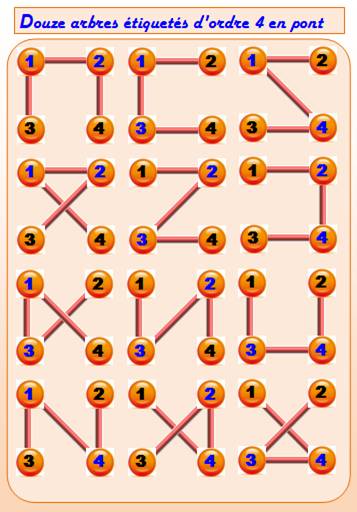
Les seize arbres étiquetés d'ordre 4

haut

Deux sortes d'arbres étiquetés avec quatre sommets:

12 en pont, et

4 en étoile.

Dans chaque cas, les sommets d'extrémités (feuilles) sont commutables (interchangeables).

Le premier en forme de pont est défini par les deux nœuds centraux 1 et 2. Les deux sommets-feuilles peuvent être indifféremment (3, 4) ou (4, 3).

Pour les deux nœuds centraux, on a tous les arrangements de quatre objets pris par deux:
Q = 4! / 2! = 24 / 2 = 12

Pour le premier en forme d'étoile, les trois sommets-feuilles sont interchangeables.

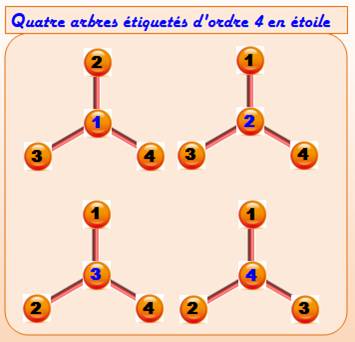
Seul le nœud central définit un arbre étiqueté. Soit quatre cas.

Bilan

12 arbres n pont et

4 arbres en étoile, soit

16 arbres étiquetés d'ordre 4

Cayley remarqua que,
pour l'ordre 4:

Q₄ = 16 = 4⁴^{– 2}

Pour information: Disposition avec étiquettes fixes

Moins immédiat à construire

Les 125 arbres étiquetés d'ordre 5

haut

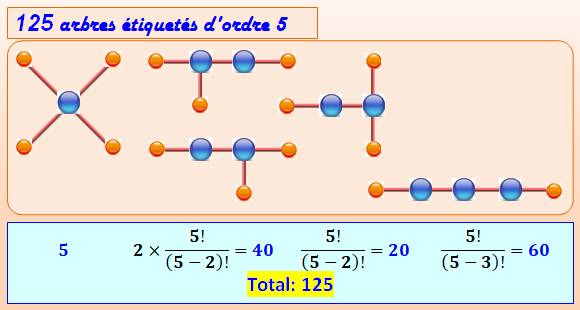
Ces arbres étiquetés à cinq nœuds sont de cinq types.

Dénombrement pour chaque type selon les possibilités d'échanges entre les nœuds centraux (en bleu).

Exemple pour la deuxième colonne:

deux cas (×2) – en haut et en bas;

pour chacun, arrangements de 2 nœuds parmi 5 valeurs possibles => 5! / (5-2)! = 120 / 6 = 20.

soit un total de: 2 × 20 = 40

Cayley remarqua que, pour l'ordre 4:

Q₅ = 125 = 5⁵^{– 2}

Arbres étiquetés – Formule de Cayley

haut

Formule de Cayley

Cayley fait une généralité de ses remarques.

Sa formule permet de calculer la quantité d'arbres étiquetés à n nœuds. Les nœuds sont numérotés 1, 2, …, n et deux arbres sont différents si leur structure ou leur numérotation est différente.

On a alors:

Quantité de graphes étiquetés
non-isomorphes:

Q = n^n–2

Historique

En 1857 James Sylvester puis en 1860, Karl Borchardt découvrent cette formule.

En 1889, Cayley la prouve en termes de théorie des graphes. C'est son nom qui va rester.

Nombres de Cayley pour n de 1 à 20

1, 1, 3, 16, 125, 1296, 16807, 262144, 4782969, 100000000, 2357947691, 61917364224, 1792160394037, 56693912375296, 1946195068359375, 72057594037927936, 2862423051509815793, 121439531096594251776, 5480386857784802185939, 262144000000000000000000.

Notez que la croissance est rapide, et vous devinez que le dénombrement (sans la formule) n'est pas très évident.

Une des formules de calcul

Programme Maple

Commentaires

Simple application de la formule indiquée.

Collecte des résultats dans la liste L.

Utilisation de l'instruction binomial qui permet le calcul des coefficients binomiaux.

Formule générale

On note Q(n, r) la quantité de graphes étiquetés avec n points et r feuilles par cette formule établie par Vites Longani.

Exemple: Q(4, 2) = 12; Q(4, 3) = 4

Q(5, 2) = 60; Q(5, 3) = 60; Q(5, 4) = 5

Q(6, 2) = 360; Q(6, 3) = 720; Q(6, 4) = 210; Q(6, 5) = 6

Tables pour
n de 3 à 10

Valeur successives de r de 2 à n – 1

3, [3]

4, [12, 4]

5, [60, 60, 5]

6, [360, 720, 210, 6]

7, [2520, 8400, 5250, 630, 7]

8, [20160, 100800, 109200, 30240, 1736, 8]

9, [181440, 1270080, 2116800, 1058400, 151704, 4536, 9]

10, [1814400, 16934400, 40219200, 31752000, 8573040, 695520, 11430, 10]

Voir Programmation – Index

Arthur Cayley (1821-1895)

Mathématicien britannique, d'abord avocat, il publie de nombreux articles de mathématiques.

En 1863, il abonne le poste lucratif d'avocat et prend un poste de mathématiques pures à Cambridge.

Inventeur des matrices dont il a développé l’algèbre. Inventeur des octonions.

En1854, il généralise la théorie des groupes au-delà des groupes de permutations. Voir Table de Cayley.

C'est lui qui introduit la notion d’espace vectoriel.

Travaux remarqués en géométrie de dimension n, en géométrie non-euclidienne et en géométrie projective.

En 1852, membre de la Royal Society.

Il est un des fondateurs de l'école britannique moderne de mathématiques pures.

Voir Contemporains

English corner

A tree is a connected, undirected graph with no cycles.

Recall that a cycle is a path that starts and ends at the same node. In a tree, there are no cycles, which means that there is only one possible path between any two nodes.

Connected means that there is a path from any node to any other node, and there is no node, or set of nodes, that is disconnected from the others.

Undirected means that there is no direction associated with an edge.

Trees introduce another set of terminology:

The root of a tree is the start node for traversals. If the tree has a root, it is called a rooted tree.

A branch is a path from the root to an end point. The end point is called a leaf.

The height of a tree is equal to the number of edges that connect the root node to the leaf node that is furthest away from it (i.e. the longest branch).

The number of edges (E) of a tree is equal to the number of nodes (N) minus one, so E = N – 1.

Sourcede l'anglais: Trees – Isaac computer science

Voir Anglais pour le bac et pour les affaires

Haut de page

Retour	Graphe planaire
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes	Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle	Percolation Relier les points d'un seul coup de crayon Table de Cayley Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	Arbre (théorie des graphes) – Wikipédia Formule de Cayley – Wikipédia Arthur Cayley – Wikipédia Trees – Lecture 1 – notes 2016 Binary Tree Data Structure – Geeksforgeeks – Description et programmation en C++ Formule de Cayley – Wikipédia OEIS A000272 – Number of trees on n labeled nodes: n^(n-2) with a(0)=1 Labeled Tree – Wolfram MathWorld Cayley Tree – Wolfram MathWorld A formula for the number of labeled trees – Vites Longani
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/ArbreE.htm