|
|||||||||||||||||||||||||||||||||||||||
![]()
|
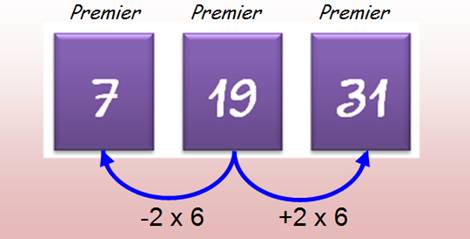
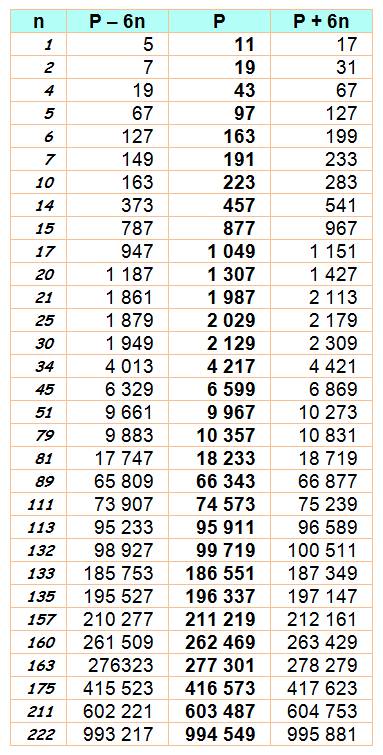
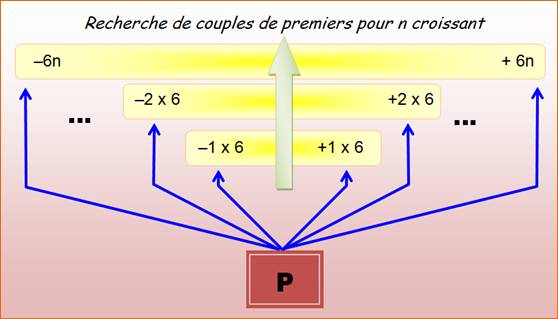
NOMBRES PREMIERS & acolytes en plus et moins 6n Prenons un nombre premier et flanquons-le
de deux premiers, l'un en +6n et l'autre en -6n.
Existe-t-il une valeur de n telle que ces deux nouveaux nombres soient
premiers? C'est le cas par exemple pour 11, car 11 + 6 = 17 et 11 – 6 = 5 qui sont tous deux premiers. Autre exemple
|
|
|
||
|
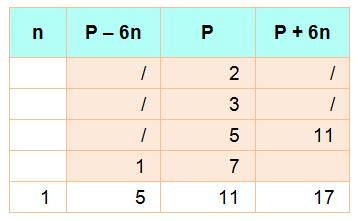
Avec 2, en ajoutant 6n, un nombre pair, le résultat sera pair
et donc non premier. Avec 3, la somme 3 + 6n sera toujours divisible par 3. Avec 5, la différence, comme pour les précédents, est
négative. Avec 7, la différence 7 – 6 = 1, nombre qui n'est pas
premier. Avec 11, nous rencontrons le premier cas recevable: 11 –
1 x 6 = 5 et 11 + 1 x 6 = 17, deux nombres premiers. Le coefficient
multiplicateur n est tout simplement égal à 1. |
|
|
|
|
||
|
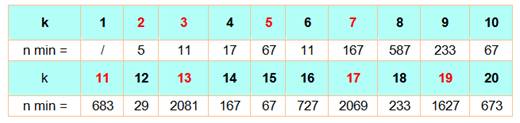
Pour tous
les nombres premiers à partir de 11 et jusqu'à 97, nous pouvons trouver deux
premiers en P – 6n et P + 6n. Et, même, la valeur du coefficient n est le
plus souvent égal à 1 er ne dépasse
pas 5. Est-ce si
extraordinaire? Pas tellement. Nous
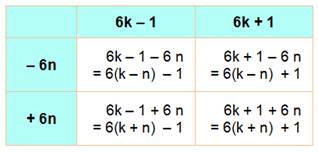
savons que tous les nombres premiers sont en 6k + 1 ou 6k – 1. Ajouter ou
soustraire 6n à ces nombre redonnent un nombre en 6K + 1 ou en 6K – 1.
Les quatre cas possibles: Ces
nombres en 6K + 1 et 6K – 1 sont potentiellement des nombres premiers, mais
pas tous. En
prenant n suffisamment grand, il est très probable de tomber sur deux nombres
premiers. |
|
|
|
|
||
|
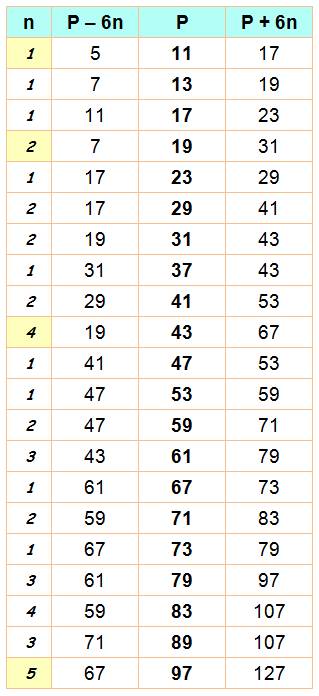
Le
tableau est construit sur le même principe que précédemment, mais on ne
conserve que les valeurs de P pour lesquelles le coefficient multiplicateur n
est plus grand que tous les précédents. On ne conserve
que les n records Tous les
nombres premiers de 11 à 1 million
réponde à notre exigence. Ils sont tous associée à deux premiers en 6n
– 1 et 6 n + 1 avec bien entendu la même valeur de n. Nous
constatons que si tous les premiers satisfont notre exigence, la valeur de n
nécessaire pour les cibler tous devient de plus grande. Avec 994 549 les deux
premiers acolytes sont très éloignées (222 x 6 = 1332). Pour le fun: 222 est un repdigit |
|
|
|
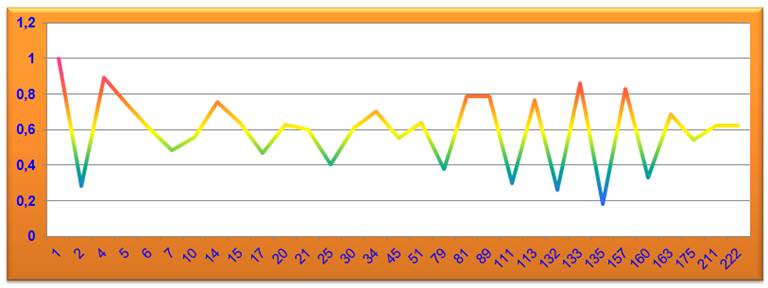
Graphe de progression En
abscisse la valeur de n et en ordonnée, le ratio de progression du nouvel
écart au précédent. Exemple pour n = 4: l'écart calculée était de 17; alors pour n = 5, l'écart
devient 67 – 17 = 50 et 50 / 67 = 0,74. Le suivant pour n = 6: 127 – 50 = 77
et 77/127 = 0,606.
Ce ratio
oscille autour de 0,6. Est-ce toujours vrai? Ce qui
voudrait dire que chaque fois qu'un nouveau record pour n survient, le nouvel
écart entre les premiers concernés est 0,6 fois l'écart cumulé précédent. |
||
|
Conjecture Pour tout nombre premier, supérieur à 7, il existe
toujours un couple de nombres premiers en P - 6n et P + 6n. Records En quelques minutes de calculateur, l'exploration jusqu'à
100 millions, montre que n maximum est égal à 569 pour P = 52 912 507 Validité Cette vérification
montre que plus P est grand, plus la valeur du coefficient n est grande. Grande jusqu'où?
Rien ne permet de dire que n
existe toujours. |
Voir Conjectures
|
|
||
|
On se
demande si cette conjecture marche avec une autre amplitude que 6n. Une
simple programmation montre que oui. Mais, ce n'est pas si étrange que cela. |
Si la conjecture en K = 6n est
vraie, alors elle vraie aussi pour toute valeur de K = kn
divisible par 6, que ce soit k ou n
qui est divisible par 6. Dit-autrement, si nous essayons P
+ 5n, nous rentrouvrons notre propriété avec n un multiple de 6. |
|
|
Bon, ça
marche, mais c'est normal. Alors, reformulons la conjecture. |
Pour tout nombre premier, supérieur à C, il existe
toujours un couple de nombres premiers en P – K et P + K, avec K multiple e 6 |
|
|
La
constante C à partir de laquelle, la conjecture semble vraie est assez variable. |
|
|
Merci
à Rabii E.G. pour la suggestion de cette conjecture
qui
a conduit à l'élaboration de cette page
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()