|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES
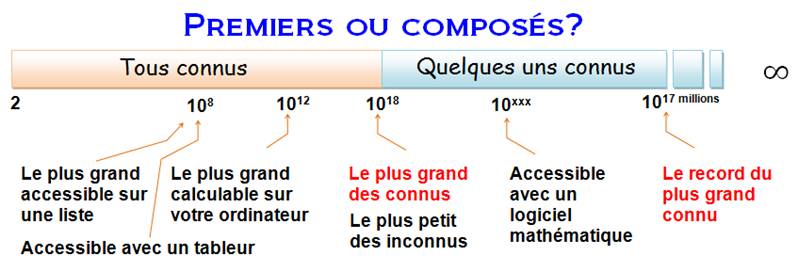
PREMIERS Les plus grands connus ou accessibles On s'intéresse
souvent au plus grand nombre premier
connu. Cependant, il en existe de nombreux autres plus petits dont on ne
sait pas s'ils sont premiers
ou composés. Où se trouve la
limite? Où s'arrête la
liste de tous les nombres connus comme étant composés ou premier? Quel est le
plus grand premier de la liste de tous les premiers consécutifs connus? Quels sont ceux qui
me sont accessibles avec mon ordinateur? |
Voir Quel type de record ?
|
|
||
|
Calculette |
Avec ma calculette, je ne peux pas aller
bien loin. Étant donné un nombre N, il me faut faire la division de N avec chacun des
nombres entiers premiers inférieurs à racine de N. |
|
|
Tables |
Internet donne accès à
des tables de nombres premiers.
|
|
Test en ligne |
Je propose deux sites
(il en existe bien d'autres):
|
|
Tableur |
Avec un tableur, il
est facile de mettre en place le crible d'Ératosthène. Excellent
exercice d'apprentissage du tableur. Il existe mieux: une formule adéquate (assez sophistiquée) qui, en
introduisant N dans une cellule, vous indique si N est premier dans la
cellule voisine. Et cela pour N jusqu'à 250 millions. |
|
Logiciels
mathématiques |
Le logiciel Maple possède une instruction
"isprime" qui indique si un nombre est premier ou non. Il peut
atteindre 10 137
000 001 (10140 milions fait déborder la capacité mémoire).
Maple indique que ce nombre n'est pas premier en 18 secondes de calcul. Cependant, ce temps de
calcul dépend largement des facteurs impliqués. En pratique, on utilisera ces
logiciels jusqu'à N = 1012. Avec les théorèmes de
théorie des nombres, on atteint 280 = 1,20…1024 sans
grande difficulté. |
|
Calculs
mémorisés en tables |
Certains laboratoires
mathématiques ont procédé au calcul de tous les nombres premiers en
conservant leur liste en mémoire
jusqu'à N = 1012. |
|
Calculs du
plus grand |
Ces laboratoires ont
épluchés les nombres jusqu'à N = 1018. Ainsi, tous les nombres premiers
successifs jusqu'à cette valeur sont connus. Intérêt pour connaître la
distance maximale (gap) entre deux premiers successifs. |
|
Records |
Sports de mathématiciens
et d'informaticiens consistant à trouver le plus grand nombre premier ou le
plus grand dans certaines catégories (jumeaux, de Saint-Germain …). Record en 2014: 2 57 885 161 – 1 avec plus de 17
millions de chiffres. Tous ces records sont en principe des nombres de Mersenne. Voir les
pages
|
|
|
|
|
Il est vrai que, plus on dépasse cette limite et plus
un ordinateur personnel prendra du temps à trouver les facteurs. Il sera un
peu plus rapide pour déterminer la primalité. |
|
Voir Brève
47-935
Bilan
|
On
retiendra les ordres de grandeur:
On
se souviendra que:
En
effet, pour savoir si un nombre est premier, il suffit de s'intéresser aux
restes de divisions (congruences);
alors pour les facteurs, il
faut absolument tout connaître du nombre. |
![]()
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()