|
||||||||||||||||||||||||||||||||||||||||
![]()
|
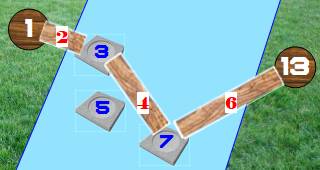
Une passerelle entre nombres pairs et nombres
premiers Conjecture des pierres de gué Une propriété bien singulière découverte
par Arnaud Debeurme; propriété qui peut aussi être l'occasion d'énigmes amusantes. Il s'agit d'atteindre un nombre
donné en ne passant que par des nombres Sur cet
exemple, on rejoint 13 en passant
par 3 et 7 (certains des premiers), avec les
passerelles 2, 4 et 6 (tous les pairs). Si la propriété semble se vérifier
du fait d'une quantité croissante de solutions, la démonstration ne m'est pas
connue. |
Pour
jouer
|
|
||
|
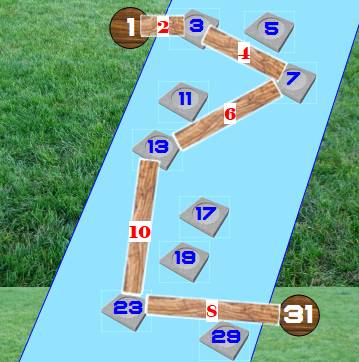
Un défi ! Comment
traverser la rivière avec ces cinq planches à poser sur les pierres de gué. Observation Avez-vous
reconnu:
Alors, si
on trouve une solution, Réponse Oui, le
passage à gué est possible ! Sans doute, sans trop de mal puisqu'il existe 17
solutions. Observations D'abord,
je fais le compte:
Ensuite
Enfin:
une question
|
Énigme Plot ou pierres de gué: nombres impairs Passerelles: planche de longueur paire
Une des solutions
|
|
|
|
||
|
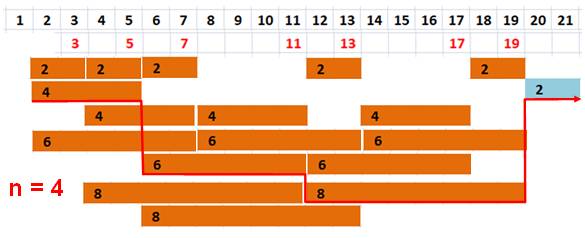
n = 4 et S = 1 + 2 + 4 + 6 + 8 = 4² + 4 + 1 = 21 Vous
devez partir ce labyrinthe
en partant du 1 et arriver au 21 en suivant un chemin horizontal ou vertical. La règle du jeu reste la même: utiliser tous les
nombres pairs et ne passer que par des nombres premiers. |
On retrouve les nombre premiers en rouge. En marron, l'écart entre ces nombres premiers. Le
dernier écart, en bleu, signale que le point d'arrivée n'est pas un nombre
premier Exemple de chemin en rouge: les quatre nombres
pairs sont bien utilisés. |
|
|
Note: le jeu serait
encore plus facile et plus divers en ajoutant les passerelles 4 entre 17 et
21 et 8 entre 13 et 21. Elles seraient montrées en bleu sur ce graphique. |
||
|
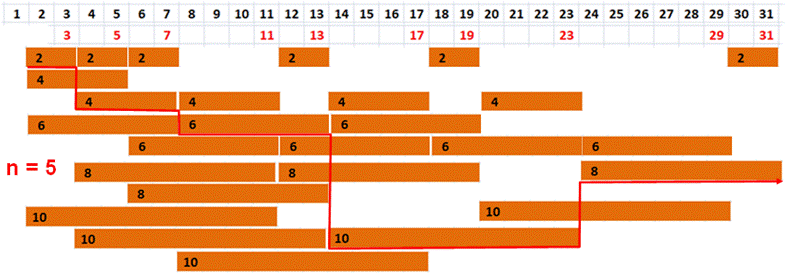
n = 5 et S = 1 + 2 + 4 + 6 + 8 + 10 = 5² + 5 + 1 = 31 Vous
devez partir du 1 et arriver au 31 en suivant un chemin horizontal ou
vertical. |
Exemple de chemin en rouge. Trouverez-vous les dix-sept possibilités ? |
|
|
|
|
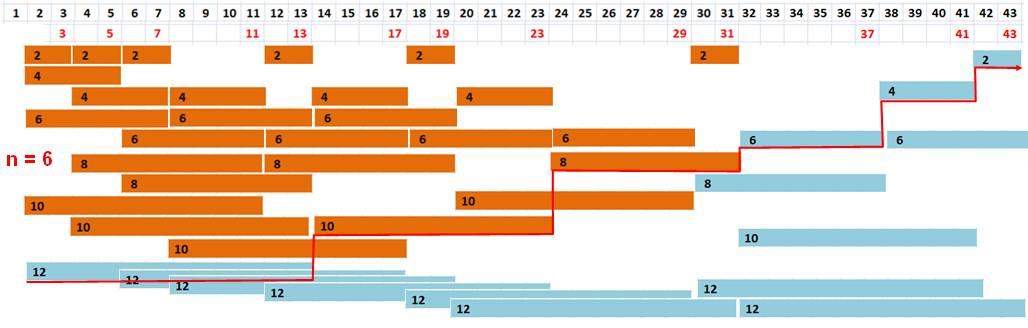
n = 6 et S = 1 + 2 + 4 + 6 + 8 + 10 + 12 = 6² + 6 + 1 = 43 Vous
devez partir du 1 et arriver au 43 en suivant un chemin horizontal ou
vertical. |
En bleu les nouveaux blocs. Si on sait faire le chemin n = 5, alors, pour n =
6, il suffit d'ajouter le bloc 12 et on est arrivé. Évidemment de nombreuses autres solutions sont
possibles. Est-ce une piste pour la solution globale de ce
défi pour tout n ? |
|
|
|
![]()
Le
coin mathématique
|
|
||
|
Somme des nombres pairs Nous
intéressons à la somme des nombres pairs de 2 à 2n. |
n = 5 S = 2 + 4 + 6 + 8 + 10 = 30 S = n² + n = 30 |
|
|
Quantité de sommes avec ordre Il existe
q = n! permutations
de cette somme. Avec 5, il y en a 5x4x3x2x1= 120, et donc autant de possibilités d'essais de
passages à gué |
Manières de
faire 30 avec ces nombres pairs (partitions
paires ordonnées)
|
|
|
Sommes cumulées Idée ! Pour chaque
permutation, on forme une nouvelle suite de nombres constituée du cumul des
termes avec initialisation à 1. Cette opération est conforme à la méthode de
passage des plots en comptabilisant la distance parcourue à chaque plot. |
[2, 4, 6, 8, 10] Devient: [1 + 2 = 3, 3 + 4
= 7, 7 + 6 = 13, En résumé: [3, 7, 13, 21,
31] Et avec les points de départ et d'arrivée: [1, 3, 7, 13, 21, 31] |
|
|
Sommes premières Observons
si ces nouveaux nombres sont premiers. Avec les
six premières partitions
de 5, deux sont formées entièrement de nombres premiers. Cette opération est conforme à la méthode de
passage des plots en ne se posant que sur des numéros premiers. |
Nombres atteints en ajoutant les nombres pairs et, ensuite,
indication si le nombre est premier (1) ou composé (0) [3, 7, 13, 21,
31], [1, 1, 1, 0, 1] [3, 7, 13, 23, 31], [1, 1, 1,
1, 1] [3, 7, 15, 21,
31], [1, 1, 0, 0, 1] [3, 7, 15, 25,
31], [1, 1, 0, 0, 1] [3, 7, 17, 23, 31], [1, 1, 1,
1, 1] [3, 7, 17, 25,
31], [1, 1, 1, 0, 1] La première solution (en jaune) est celle illustrée en introduction. |
|
|
|
||
|
Conjecture 1 Pour tout
n, il existe au moins une telle suite première réalisée à partir des partitions paires ordonnées du nombre n² +
n. Vérifiée pour n jusqu'à 150. |
Avec n = 5, sur les 120 partitions ordonnées, il existe 17 suites
premières:
|
|
|
Conjecture 2 Pour tout
n, tous les nombres premiers entre 3 et S se retrouvent parmi ces suites
premières. Vérifiée pour n jusqu'à 150. |
Avec n = 5, S = n² + n + 1 = 31 Liste des nombres premiers avec en indice la quantité de fois présents
dans les suites premières de n: [34,
56, 77, 117, 1310, 176,
198, 2313, 295] Chacun des nombres premiers est présent de multiple fois. |
|
|
Conjecture 3 et 4 Vérifiée pour n jusqu'à 100. |
Les
conjectures 1 et 2 sont vraies si on utilise les nombres chanceux comme pierres de gué. Les
conjectures 1 et 2 sont vraies si on utilise les nombres pratiques comme pierres de gué pour
aller de 0 à n² + n. |
|
Voir Conjectures
|
|
||||||||||||||||||||||||||||||||
|
Table pour n de 2 à 10 La
quantité de partitions en nombres pairs avec prise en compte de l'ordre croit
très rapidement. La
quantité de suites premières suit ce rythme. On y trouve bien tous les
nombres premiers entre 3 et S. Cette
vérification jusqu'à 10 laisse penser qu'il existe toujours de telles suites
premières. Est-ce
que la preuve est simple ou très complexe ? |
|
|||||||||||||||||||||||||||||||
|
|
||
|
Récurrence S'il
existe une solution pour n, est-ce qu'il existe aussi une solution pour n + 1
? De part le principe de la construction de passage
de gué ou de labyrinthe, dès que l'on dispose d'un chemin valide pour n, on
dispose d'un chemin pour n + 1 en prolongeant le chemin pour n avec le
nouveau nombre pair à disposition. |
Exemple L'objectif S augmente de 12
et, justement, le nombre 12 a été ajouté. Ayant une solution pour 5, on dispose également
d'une solution pour 6. Il suffit d'ajouter 12 en fin de parcours du 5. |
|
|
Oups ! Cette affirmation viendrait clore la preuve si
tous les points de destination étaient des nombres premiers, or il en existe
beaucoup de composés. |
Valeurs de S pour les n
successifs: En rouge les nombres composés: 3, 7, 13, 21, 31,
43, 57, 73, 91, 111, 133,
157, 183, 211, 241, … |
|
|
Il semble que les nombres premiers soient des points
passerelles pour les nombres pairs successifs, le point d'arrivée étant un
nombre composé ou premier. Lorsque, pour n, le point final est premier, alors il existe
une solution certaine pour n+1 si on
connaît une solution pour n. Le fait que le point final puisse être un nombre
composé n'autorise pas de clore la preuve de cette propriété avec ce
raisonnement par récurrence. Quelles sont les pistes?
|
![]()
|
Somme des pairs + 1 =
premier ? |
|
|||||||||||||||
|
Est-il
courant pour n² + n + 1 d'être
premier? Non ! Ils
sont de plus en plus rares. |
|
|||||||||||||||
|
Distribution des nombres
premiers |
|
|
|
Question Parmi
tous les nombres premiers d'une plage de 1 à n, quels sont tous les écarts
possibles entre ces nombres et y retrouvent-on toujours tous les nombres
pairs ? Réponse Un test par
programme montre que (du moins pour la partie testée): Entre 3 et 2n, tous les écarts entre nombres
premiers couvrent bien la plage des nombres pairs de 2 à 2n. |
Exemple Avec n = 5 et jusqu'à 31, on trouve dix nombres premiers [3, 5, 7, 11, 13, 17, 19, 23, 29, 31] dont les écarts entre eux sont: 5 – 3 = 2; 11 – 5 = 4;
17 – 11 = 6; 19 – 11 = 8 et 29 – 19 = 10 Soit tous les nombres pairs de la plage (de 2 à 2n = 10), au moins une
fois. |
|
Page publiée avec
l'autorisation d'Arnaud
Debeurme, l'auteur de
cette originalité:
|
|
||
|
Is there a
relation between prime numbers and even numbers? It would seem so. This is
the conjecture of the "ford crossing" proposed by Arnaud Debeurme
in April 2020. Let be the
sequence of even numbers from 2 to 2n. The sum is S = n² + n. The goal is
to build a path which starts from 1 and reaches S + 1 while progressing among
the prime numbers of this interval. The conjecture says that there exists at least a path
such that the distances between all these numbers (starting number, primes
and end number) make up the sequence of even numbers. |
Existe-t-il une relation entre les nombres premiers et
les nombres pairs? Il semblerait que oui. C'est la conjecture du passage de
gué proposée par Arnaud
Debeurme en avril 2020. Soit la suite des nombres pairs de 2
à 2n. La somme vaut S = n² + n. Le but est de construire une chemin
qui part de 1 et atteint S + 1 en progressant parmi les nombres premiers de
cet intervalle. La conjecture dit qu'il existe au
moins un itinéraire tel que les distances entre tous ces nombres (départ,
premiers et arrivée) constituent la suite des nombres pairs. |
|
![]()
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()