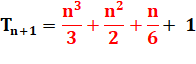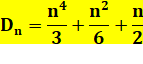|
Édition du: 03/07/2023 |
|
INDEX |
Énigmes algébriques |
|||
![]()
|
Somme de la diagonale d'un tableau (matrice) Comment calculer
la somme de la diagonale de tableaux carrés de plus en plus grand ? Notre défi: En
fonction de n, calculer la valeur du nombre de tête (T) et la somme de la
diagonale (S).
Voir Brève
793 |
||
|
|
Sommaire de cette page >>> Approche
>>> Valeur de tête >>> Somme de la diagonale >>> Bonus: calcul de la valeur de tête |
Débutants Glossaire |
|
Problème Un tableau carré de 4 x 4 = n². Les nombres se succèdent à partir d'une valeur de
départ T. Quelle est la somme D de la diagonale de ce
tableau en fonction de T et de n ? Solution D = 15 + 20 + 25 + 30 = 4 x 15 + (0 + 5 + 10 + 15) = 4 x
15 + 5 (0 + 1 + 2 + 3) Avec la somme des entiers
de 0 à 3 avec 3 = n – 1:
Ici, on retrouve: 4x15 + 64/2 – 4/2 = 60 + 32 – 2
= 90 |
= 4 x 15 +
|
|
|
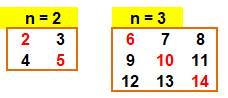
Problème Connaissant Tn = 2 pour n = 2, calculer Tn+1 = 6
pour n = 3. Puis, donner la valeur de T en fonction de n. Formule de récurrence Il s'agit simplement d'ajouter le carré de n à la
valeur de départ pour obtenir celle d'arrivée. Ici pour n = 2: 6 = 2 + 2²; Pour la suivante avec n = 3: 6 + 9 = 15 Formule absolue L’addition en tableau montre que la valeur de
tête Tn+1 est égale à la somme des carrés + 1. Or la somme des
carrés vaut:
Tous calculs faits pour Tn:
Pour n = 4: T = 27/3 + 9/2 + 3/6 + 1 = 15 |
Deux tableaux successifs
Calcul de la valeur de tête
|
|
|
Avec ces deux formules, nous sommes en mesure de
calculer la somme de la diagonale de n'importe quel tableau de dimension n. |
|
||
|
Après fusion, la formule devient excessivement
simple. |
|
||
|
Valeur pour n jusqu'à 20 [n, T, S] |
[1, 1, 1], [2, 2, 7], [3, 6, 30], [4, 15, 90],
[5, 31, 215], [6, 56, 441], [7, 92, 812], [8, 141, 1380], [9, 205, 2205],
[10, 286, 3355], [11, 386, 4906], [12, 507, 6942], [13, 651, 9555], [14, 820,
12845], [15, 1016, 16920], [16, 1241, 21896], [17, 1497, 27897], [18, 1786,
35055], [19, 2110, 43510], [20, 2471, 53410], … |
||
|
Formule Je ne connais pas la formule de la somme des
carrés. Comment retrouver la formule de la valeur de tête? Il faut résoudre un système d'équations
à quatre inconnues |
|
||
|
Analyse des différences successives En prenant les premiers exemples du tableau
ci-dessous (jusqu'à n = 5 ou 6, cela suffit), on examine la progression des
valeurs (la différence entre une valeur et la valeur précédente) On recommence jusqu'à ce que les différences
soient constantes. Il faut trois tours.
L'équation qui représente T est donc du troisième
degré. Sa forme générique est: Il s'agit de trouver les valeurs de a, b, c et d
en confrontant l'équation à quatre valeurs connues. Le calcul est présenté dans le tableau de droite. |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |