|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Rectangles magiques IMPAIRS Exemples et construction Exemples
de rectangles magiques impairs.
Leur construction s'avère extrêmement difficile sans l'aide des ordinateurs et d'algorithmes élaborés. Les
auteurs en référence proposent la construction des
rectangles magiques m x m+2 avec m
impair en utilisant des tableaux de
nombres (matrices). |
|
|
||
|
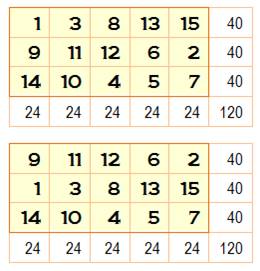
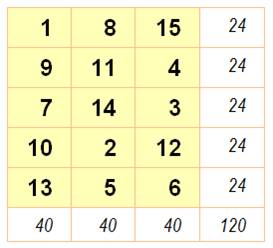
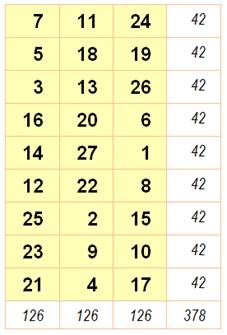
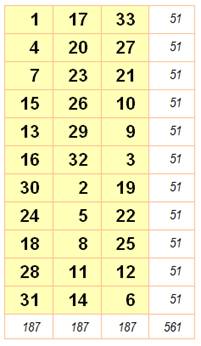
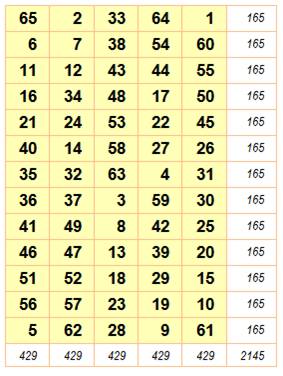
Rectangle 3x5 Données magiques m = 5, n
= 3 N de 1 à
3x5 = 15 S =
½ 15 x 16 = 120 M = ½ (3
x 5 + 1) = 8 SL = 5 x 8 = 40 SC = 3 x
8 = 24 Rappel: Normal: tous les nombres de 1 à mn. Associatif: somme constante avec les extrémités des
diagonales. Voir Données
magiques |
Rectangle 3x5 normal puis normal et associatif
Suite sur le Rectangle 3 x 5 |
|
|
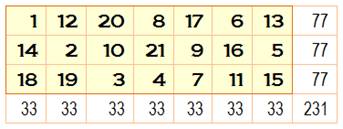
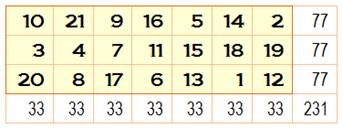
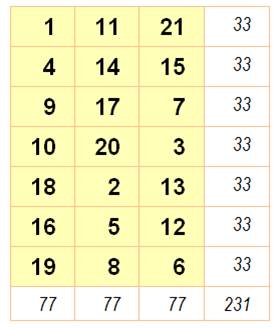
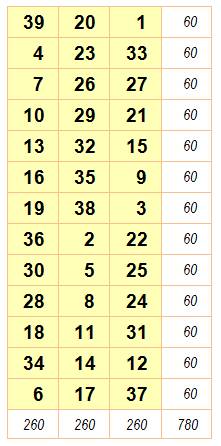
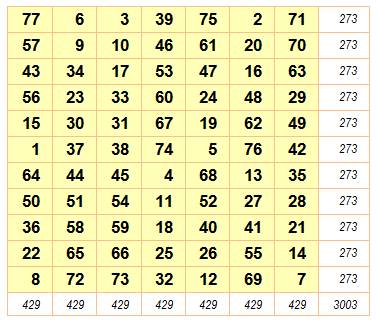
Rectangle 3x7 Données magiques m = 7, n
= 3 N de 1 à
3x7 = 21 S =
½ 21 x 22 = 231 M = ½ (3
x 7 + 1) = 11 SL = 7 x 11 = 77 SC = 3 x
11 = 33 |
Rectangle 3 x 7 normal puis normal et associatif
|
|
|
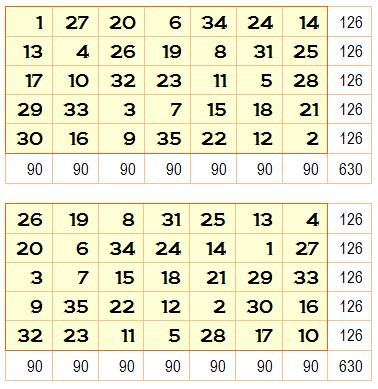
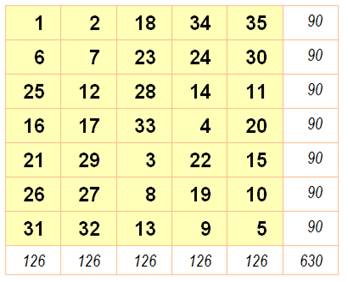
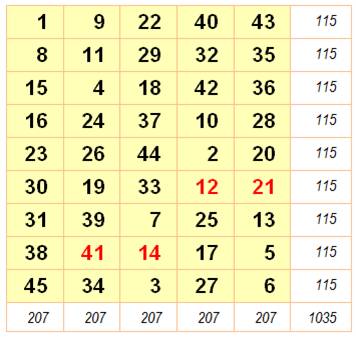
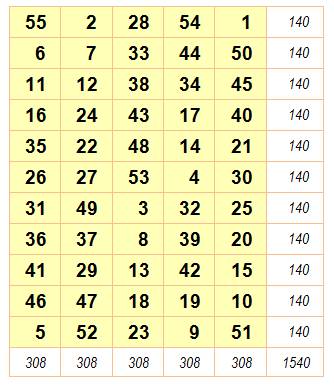
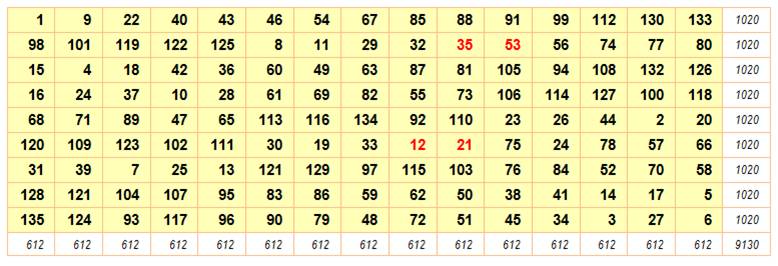
Rectangle 5x7 Données magiques m = 7, n
= 5 N de 1 à
5x7 = 35 S =
½ 35 x 36 = 630 M = ½ (5
x 7 + 1) = 18 SL = 7 x 18 = 126 SC = 5 x 18 = 90 |
Rectangle 5 x 7 normal puis normal et associatif
|
|
|
|
|
|
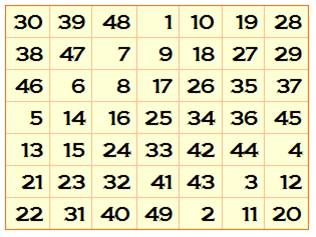
Distribution régulière En
adoptant un remplissage haut-bas et gauche-droite, on obtient un rectangle
presque magique.
Reste à
déformer ce bel ensemble pour en faire un vrai rectangle magique. Pas facile!
Exemple de
déformation pour arriver à la solution
Solution trouvée
par Arsène Durupt Sommes magiques respectées En adoptant
un remplissage gauche-droite et haut-bas, on obtient un rectangle presque
magique. Reste à déformer ce bel ensemble pour en faire un vrai rectangle
magique. Pas facile!
|
|
Point de situation
|
On
peut obtenir assez rapidement un rectangle presque magique. Reste à
travailler le tableau pour conserver les sommes magiques tout en introduisant
les nombres manquants. C'est
l'objet de la méthode indiquée ci-dessous qui est due aux auteurs dont les
textes sont cités en référence. |
|
|
||
|
La
méthode est décrite dans cette colonne |
Avec
exemple d'application dans cette colonne |
|
|
1)
Construire la matrice Jm x m
avec Jij = 1 |
Exemple R 7x9
|
|
|
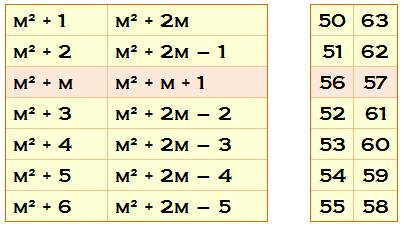
2)
Construire la matrice Am x m avec aij = j + i + (m – 3)/2 mod m Exemple de calcul a11 = 1 + 1 +
(7 – 3)/2 mod 7 a77 = 7 + 7 +
(7 – 3)/2 mod 7 |
|
|
|
3)
Construire la matrice Bm x m
avec bij = 2(j – 1) + i mod m |
|
|
|
4)
Construire la matrice Cm x m avec m.A + B + J |
|
|
|
Détail du
calcul |
|
|
5)
Construire la matrice D2 x m avec |
|
|
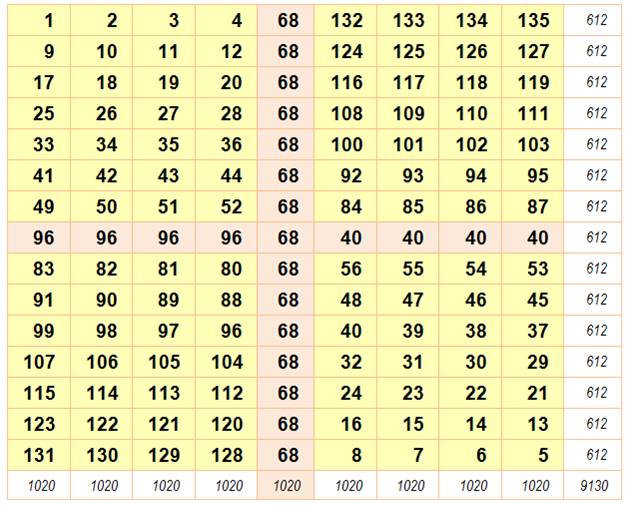
6)
Construire les matrices C1 et D1 résultant des échanges suivants: Pour i de 1 à (m – 1)/2 échangez |
|
|
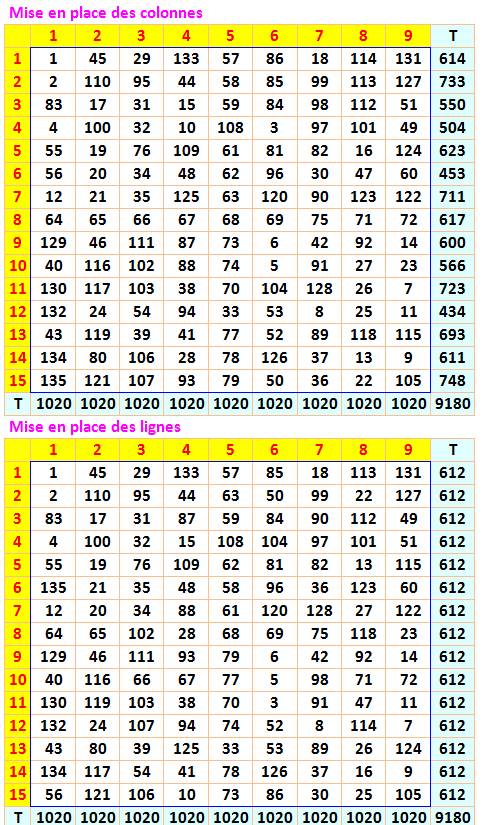
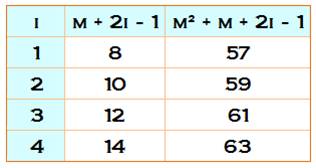
7)
Construire les matrices C2 et D2 résultant des échanges suivants: Pour i de 1 à (m + 1)/2 échangez |
|
|
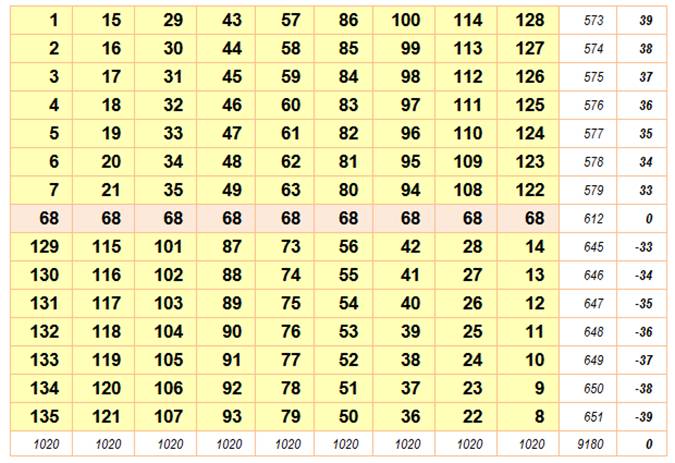
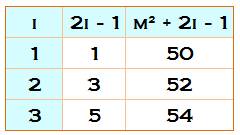
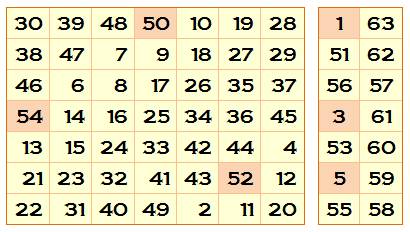
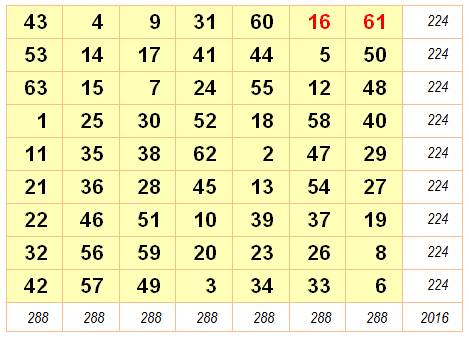
8)
Construire la matrice R en juxtaposant
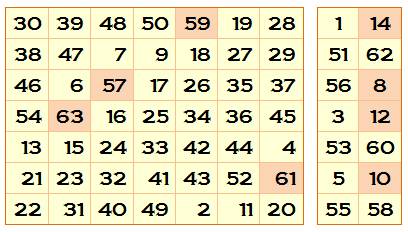
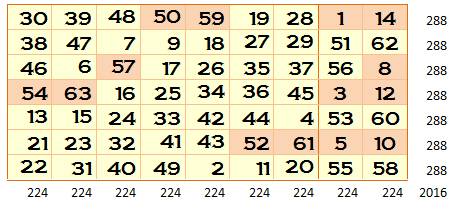
C2 et D2. Données magiques m = 9, n
= 7 N de 1 à
7x9 = 63 S = ½
63 x 64 = 2016 M = ½ (7 x 9 + 1) = 32 SL = 9 x 32 = 288 SC = 7 x 32 = 224 |
|
![]()
|
3 x 9
|
7 x 9
|
|
3 x 11
|
9 x 11
|
|
3 x 13
|
5 x 11
|
|
5 x 13
|
7 x 11
|
Tous les rectangles magiques de cette collection on été
obtenus avec le générateur cité en référence
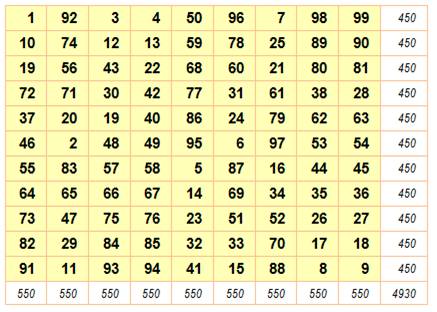
Un spécimen de 15 x 17
créé par Arsène Durupt
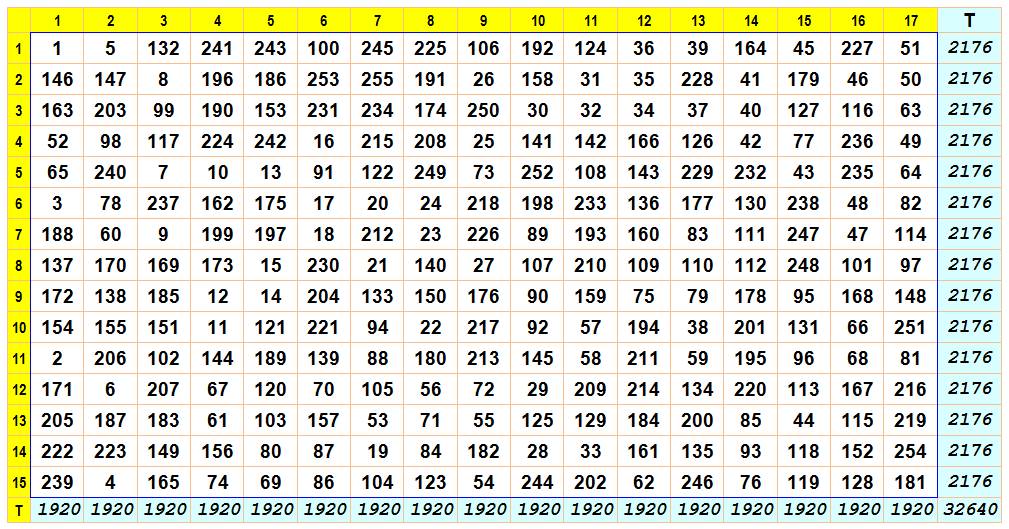
Notez que 1, 2 et 3 sont en colonne
1, puis 4, 5 et 6 en colonne 2, etc. jusqu'à 49 50 et 51 en colonne 17.
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/RecMagIM.htm |
![]()