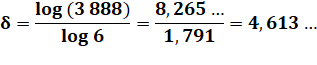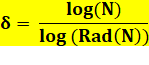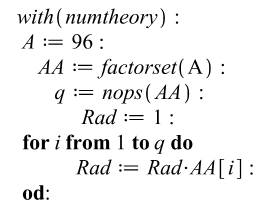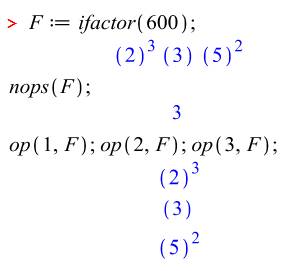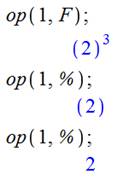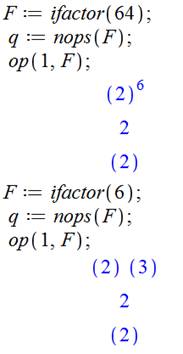Ce site est désormais accessible en http://diconombre.fr/index.html et pour cette page voir le lien en fin de page For this page, refer to the link at the bottom.

22 Novembre 2025

NOMBRES – Curiosités, Théorie et Usages

Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2026

Orientation générale  DicoMot Math Atlas Actualités M'écrire

Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

FACTORISATION

Débutants

Multiplication

Conjecture ABC

Glossaire

Facteurs et Diviseurs

INDEX

Facteurs et diviseurs

Facteurs

Nombres riches

Conjecture

Commentaires

Signature

Facteurs communs

Facteurs et Exposants

Chiffres dans facteurs

Sommaire de cette page

>>> Approche

>>> Définition

>>> Propriétés

>>> Table pour les nombres de 1 à 100

>>> Courbe de richesse

>>> Programmation

NOMBRES RICHES

Les entiers se décomposent en facteurs, chacun porté à une puissance. Si ces puissances sont grandes, le nombre est riche.

Voir Nombres plénipotents

Approche
Un nombre à une puissance élevée est un nombre riche. 1024 = 2^10 ; 531 441 = 3^12 ; 30517578125 = 5^15 … Le produit de tels nombres est un nombre riche. 3 888 = 2^4 x 3^5 ; 7 938 000 = 2^4 x 3^4 x 5^3 x 7^2 Les nombres riches sont rares. La somme de deux nombres riches est rarement riche (objet de la conjecture ABC).

Définition de la richesse d'un nombre
Un nombre est riche si un de ses facteurs au moins est répété deux fois ou plus.	4 = 2^2 12 = 2^2 x 3 90 = 2 x 3^2 x 5 540 = 2^2 x 3^3 x 5
Soit un nombre riche et sa décomposition en facteurs. On se pose la question: quelle serait la puissance moyenne de ce nombre? comment choisir les valeurs?	3 888 = 2^4 x 3^5 3 888 =
On prend tout simplement le radical de ce nombre. Et la puissance qui, appliquée au radical redonne le nombre.	Rad (3 888) = 2 x 3 = 6 3 888 =
En prenant le logarithme. Sachant que le log de a^b est simplement b log a.	log (3 888) = x log 6
Nous venons de formuler une puissance moyenne relative à 3 888, c'est sa richesse: delta = 4,613…
Richesse d'un nombre: puissance telle que le nombre est égal au radical élevé à cette puissance.

Propriétés

Les nombres les plus riches sont les puissances pures. Le nombre 64 = 2^6, pourtant inférieur à 100, atteint déjà une richesse de 6. Ensuite, viennent les nombres puissants. Notamment les puissances de 10 en 2^p x 5^p dont la richesse est p. Ils sont plus nombreux que ceux en puissance pure. Les presque puissants, sont un peu plus nombreux et possède une richesse au dessus de la moyenne. Ces nombres sont relativement rares. Les nombres où les facteurs se répètent sont assez rares. Le graphique ci-dessous montre que la richesse stage en dessous de 2 avec quelques points qui dépassent. C'est pourquoi, si nous choisissons deux riches, la probabilité pour que leur somme soit riche est vraiment très faible. La moyenne de la richesse des nombres se situe à environ 1, 04 et on pense qu'elle ne dépasse par 1, 06. Bilan La conjecture ABC s'intéresse aux couples de nombres riches et se pose la question de la richesse de leur somme.

Table des nombres de 1 à 100

Pour chaque nombre: q indique la quantité de facteurs; Rad, la valeur du radical (produit des facteurs sans répétition); Richesse exprime la richesse du nombre telle que définie ci-dessus (une sorte de puissance moyenne du radical) et en colonne de droite, la liste des facteurs. Pour le nombre 1, la richesse n'est pas définie, car le log de 1 est nul et il est impossible de diviser par 0. Pour les puissances pures, on trouve naturellement que le radical est l'argument et la richesse l'exposant. Pour 64 = 2^6 : Radical = 2 et Richesse = log(2^6) / log (2) = 6 log(2) / log (2) = 6. Outre les puissances pures dont la richesse est aussi grande qu'on le veut, la deuxième série qui tient les records sont tous les nombres en 2^p x 3^q car le nombre croit et le radical reste à 6, le minimum possible. La suite de tels nombres: 12, 18, 24, 36, 48, 54, 72, 96 …

Voir Tables – Index

Programmation – Présentation des deux méthodes

Comment trouver les facteurs d'un nombre, calculer son radical et évaluer sa richesse? Deux manières de s'y prendre sont présentées.

La première est très directe. Elle utilise une instruction toute faite: factorset qui donne la liste des facteurs.

La seconde, avec ifactor, est un exercice pratique qui permet de se familiariser avec la manipulation des listes et l'extraction d'entités enfouies dans une liste ou dans des parenthèses.

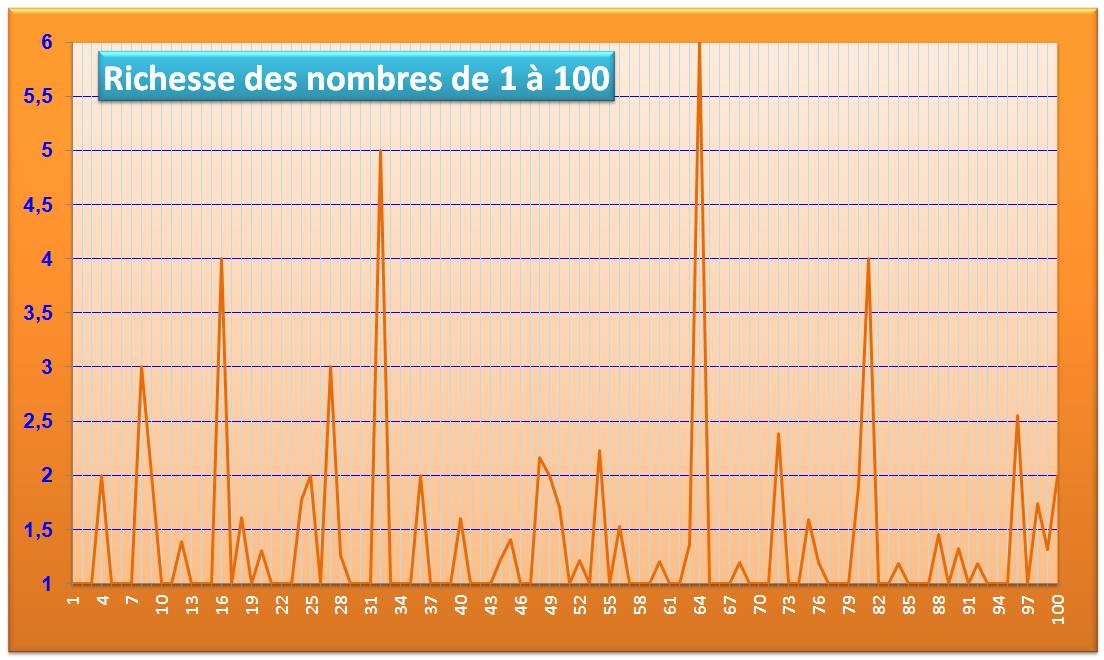
La seconde est organisée pour calculer ces paramètres sur tous les nombres de 1 à 100.

La programmation utilise le logiciel Maple.

Voir Extraction des facteurs d'un nombre et de son plus grand facteur

Programmation – Avec factorset
	Appel au package de théorie des nombres. Exemple avec 96, placé dans la variable A. Demande de la liste des facteurs, placée dans AA. Calcul dans q de la quantité de facteurs. Initialisation du radical à 1. Boucle qui ferait q tours, autant que de facteurs. Le pointeur i indique le numéro de la boucle, soit le rang du facteur Le radical est multiplié par le nouveau facteur (N°i). Fin de la boucle Précaution de non division par 0 au cas où Rad vaudrait 1. Son logarithme serait 0 et R non calculable. Calcul de la richesse (ratio des logarithmes) selon la définition. RR est une évaluation de la richesse avec cinq chiffres Impression des résultats de calcul. En bleu, valeur du nombre (A = 96), de son radical (Rad = 6) et de sa richesse (RR = 2,5473…)

Programmation avec ifactor (comme exercice de programmation avec des listes) – Explications liminaires
Isoler les facteurs	Comment extraire les facteurs d'un nombre? Nous allons utiliser l'instruction ifactor qui produit les facteurs d'un nombre sous la forme indiquée pour 600. Le problème consiste à extraire les facteurs 2, 3 et 5. À ma connaissance aucune instruction simple du package Maple ne sait faire. L'instruction nops permet de compter les facteurs. Nous pouvons alors explorer les facteurs l'un après l'autre, de 1 à q. L'instruction op sert à isoler les éléments de la liste. Mais l'instruction nous sort tout. Alors que faire?
Extraire les facteurs	Il nous faut poursuivre l'extraction: Le premier op donne (2)^3 Le second puise un cran plus loin: (2) Le troisième, pioche le 2 dans les parenthèses. Souvenez-vous que % est la valeur du dernier calcul
Cas des puissances pures	Dans le cas des puissances pures, Mapple, indique qu'il a deux termes, comme dans un produit tout simple. Cette logique m'échappe, mais il faut faire face! Avec 64 = 2^6, nous optons q = 2 facteurs, ce qui me semble étrange! L'extraction du premier terme donne (2). Avec 6 = 2 x 3, nous avons q = 2 facteurs, ce qui est logique. L'extraction du premier terme donne (2). Notre programme devra détecter les cas de fréquences pures. Nous allons isoler les deux premiers facteurs et comparer au nombre. Avec 2 et 6, 2^6 est comparé à 64 => puissance; Avec 2 et 3, 2^3 est comparé à 6 => facteurs.

Programmation – Programme complet
with(numtheory)	Boucle de balayage des nombres de 1 à 100. F est la liste des facteurs. q est la quantité des facteurs. Le radical est initialisé à la valeur 1. Boucle d'extraction des facteurs de 1 à q. Extraction en trois fois du nombre exprimant le facteur (cf. ci-dessus). Les deux premiers facteurs sont mis en mémoire (F1 et F2). On calcule la puissance F2 de F1 pour détecter une fréquence pure. Calcul itératif du radical: progression à chaque boucle. Sauf si puissance pure, alors le radical est égal au premier facteur trouvé. Précaution de non division par 0 au cas où Rad vaudrait 1 et son logarithme 0. Calcul de la richesse (ratio des logarithmes) selon la définition. RR est une évaluation de la richesse avec cinq chiffres Impression des résultats de calcul. Fin de la boucle (do à l'envers) d'exploration des nombres.

Voir Programmation / Manipulation des listes

Suite	Conjecture ABC
Voir	Facteurs et diviseurs Les riches
Cette page	http://diconombre.fr/aMaths/Factorisation/Riches.htm