|
||||||||||||||||||||||||||||||||||
![]()
|
Théorie
des ensembles SOUS-ENSEMBLES En séparant un ensemble en plusieurs parties, on
forme des morceaux d'ensemble, des sous-ensembles. Tous les éléments d'un sous ensemble S de
l'ensemble E appartiennent à l'ensemble E. |
|
|
||
|
C est un
sous-ensemble de S qui lui-même est un sous-ensemble de E. C est un
sous-ensemble de S et de E. On peut le noter de cette manière:
|
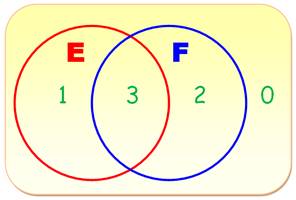
Exemples E = {1, 2, 3, 4, 5} S = {1, 3,
5} T = {1, 5, 6, 7} A = {2, 3, 1, 4, 5} B = { 2,
4 } C = {1, } S est un sous-ensemble
de E. T n'est pas un
sous-ensemble de S. A est égal à E, a
fortiori, il est inclus dans E. S et B sont
complémentaires, car réunis ils donnent E. Notations
|
|
|
|
||
|
Propriétés évidentes
Propriétés avancées
|
Formulation
Si
Alors Si
Alors |
|
|
|
||
|
M = H
C = L |
Exemple
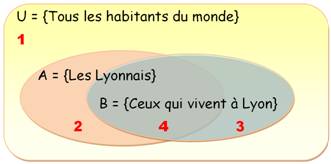
U = 1 = ensemble des habitants du monde; A = 2 B = 3 2 = Les Lyonnais qui n'habitent pas Lyon; 3 = les habitants de Lyon qui ne sont pas de
souche lyonnaise; 4 = A 1 1 2 |
|
Voir Exemples en parties d'un
ensemble
|
|
||
|
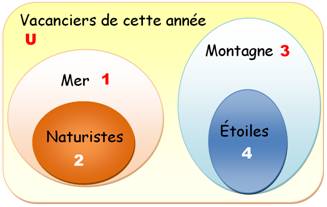
Le diagramme de Venn
est montré ci-contre. Affirmations 1 – Cette année, parmi les vacanciers
certains ont choisi montagne et d'autres la mer. 2 – Seuls ceux qui sont partis à la mer font
du naturisme. 3 – Seuls ceux qui sont à la montagne
observent les étoiles. Conclusion – Les naturistes ne regardent pas
les étoiles et ceux qui sont passionnés par les étoiles ne sont pas
naturistes. Définition
|
Diagramme
Explications L'ensemble des vacanciers de cette année
constitue l'ensemble plein (U). Ceux qui vont à la mer ne sont pas ceux qui
vont à la montagne. Ils constituent deux ensembles bien séparés: ils sont disjoints.
Ces deux ensembles ne remplissent pas l'ensemble plein. Il y, par
exemple, ceux qui restent chez eux. Parmi ceux qui sont à la mer, il y a les
adeptes du naturiste et les autres. L'ensemble naturistes (2) est inclus dans
l'ensemble mer. De même, l'ensemble observateurs des étoiles
(4) est inclus dans l'ensemble montagne (3). Les ensembles (2) et (4) sont manifestement disjoints. D'où la conclusion: les naturistes ne
regardent pas les étoile et ceux qui regardent les étoiles ne sont pas
naturistes. |
|
|
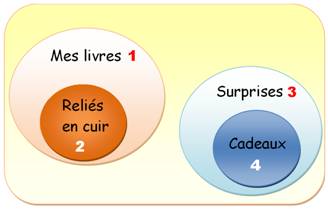
Un autre exemple Affirmations 1 – Mes livres sont les seules choses
reliées en cuir que je possède. 2 – Les cadeaux de ma sœur sont toujours
surprenants. 3 – Aucun de mes livres n'a été une
surprise. C – Les cadeaux de ma sœur ne sont pas des
objets reliés en cuir. |
Diagramme
Explications (On omet le mot "ensemble" pour alléger le texte). Parmi mes livres (1), certains sont reliés
en cuir (2), mais pas tous. Par contre, tout ce qui est relié en cuir est un
livre. Donc: 2 Parmi les surprises (3) qui me sont faites,
il y les cadeaux de ma sœur (4). Et tous ses cadeaux sont des surprises.
Donc: 4 Les livres et les surprises n'ont aucun
point commun. Donc: 1
est 3 sont disjoints. Donc, les cadeaux de ma sœur ne sont jamais
des objets reliés en cuir. En effet: 2 et 4 sont disjoints. |
|
|
||
|
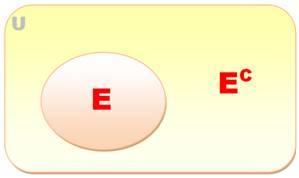
Complémentaire
Différence
Différence double (ou symétrique)
|
Complémentaire
Complémentaire = Différence
Différence = E\F = E
– F Différence double
Différence double = E = (E \
F) = (E |
|
|
|
||
|
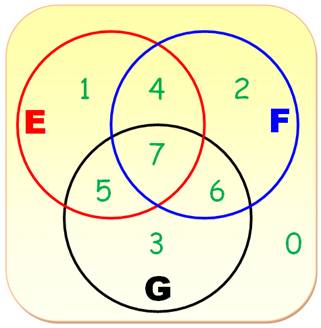
Avec deux ensembles
Avec trois ensembles
|
|
|
Voir OU Exclusif / Quatre
ensembles
|
|
|
|
|
|
|
Un sous-ensemble de E est un
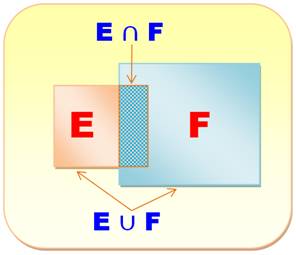
ensemble dont tous les éléments appartiennent aussi à E. Deux ensembles sans élément commun sont DISJOINTS. Dans le cas contraire, leur globalité est appelé UNION et leurs éléments communs forment l'INTERSECTION des deux ensembles. Nous avons aussi défini les ensembles complémentaires,
différence ou encore double différence. Le diagramme de Venn est une
représentation topologique, une figure, qui facilite le suivi d'un
raisonnement logique. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()