NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/11/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Jeux et énigmes
Débutants Général	JEUX DE SOCIÉTÉ				Glossaire Général
INDEX Jeux Dénombrement Grands nombres	Rubik	Solitaire	Échecs	Roulette
	Morpion	Jeu de l'oie	Plateau	Pousse
	421	Tangram
	Terminale	Sommaire de cette page >>> Jeu de dés – 421 >>> Énigme >>> Calcul de probabilité – Premier lancer >>> Configurations différentes – Curiosité >>> Deux bons au premier lancer >>> Un seul bon chiffre au premier lancer >>> Tableau des possibilités pour atteindre 421 >>> Cas G21 >>> Cas G201 >>> Cas G12 >>> Cas G111 >>> Tableau des probabilités >>> Simulation

Jeu de dés - 421
Jeu du quatre cent vingt et un ou quatre vingt et un. Jeu de dés dérivé du zanzibar, et où la combinaison la plus forte est le 4, le 2 et l'as. Le score le plus élevé: 421 en seul lancé: 10 points. Le score le moins élevé: 221, dit nénette.	Le jeu en bref Il consiste à lancer les trois dés simultanément et cela jusqu'à trois fois pour obtenir la meilleure combinaison. Lors du deuxième et du troisième lancer, il est possible de conserver un ou deux dés sur la table. Par exemple: L1 => 135 => 1 conservé. L2 => 45 => 1 et 4 conservés. L3 => 2 => 421 bingo!

Énigme
Le nombre 421 est premier. Chaque dé joué est un cube. Or le cube possède 13 axes de symétries.	D'où la formulation d'une énigme proposée par la revue Tangente (N°153): Trouver un nombre premier dont chaque partie met en jeu trois polyèdres réguliers identiques possédant chacun treize axes de symétries.

Calcul de probabilité – Premier lancer de dés
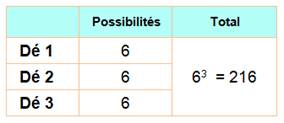
Un lancer de trois dés conduit à 216 présentations possibles. Résultats indépendants sur chaque dé. Ils sont lancés simultanément mais pourraient l'être l'un après l'autre.	Trois dés lancés produisent 216 présentations possibles.
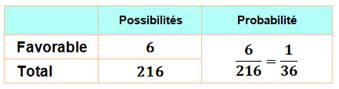
Probabilité du 421 au premier lancer. Six présentations sur 216 font l'affaire: 124, 142, 214, 241, 412 et 421.
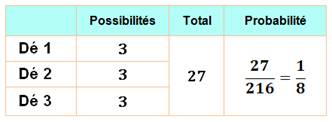
Aucun bon numéro au premier lancer. Chaque dé peut prendre les valeurs: {3, 5, 6}. Soit 3 x 3 x 3 = 27

Bilan

Lors d'un premier lancer, nous savons qu'il existe 216 possibilités avec:

6 cas pour obtenir 421 du premier coup,

27 cas pour ne rien obtenir du tout, et

183 cas pour obtenir un bon chiffre ou deux bons chiffres.

Voyons combien de cas à un et deux chiffres.

Configurations différentes – Curiosité
Au sens du 421, l'ordre n'est pas pris en compte. Type1: {111} Type 2: {112, 121, 211 …} Six fois le chiffre répété et cinq possibilités à chaque fois. Type 3: {123, 132, 231, …} Tirage de trois chiffres différents parmi 6. Vérification 6 x 1 + 30 x 3 + 20 x 6 = 216	Parmi toutes les présentations certaines sont identiques lorsque l'ordre n'est pas pris en compte. Il existe alors 56 configurations différentes.

Abréviation: 12$ veut dire chiffre 1 sur le dé 1, chiffre 2 sur le dé 2 et chiffre quelconque sur dé 3.

Deux chiffres bons au premier lancer
Ce cas n'est pas très difficile mais nécessite un bon sens de l'observation! Trois cas se présentent: 12, 14 ou 24. Commençons par le cas où nous tirons les chiffres 1 et 2. Il y a 6 cas: 12$, 21$, 1$2, 2$1, $12 et $21; Pour 12$, $ = {1, 2, 3, 5, 6}. Soit 5 possibilités. $ = 4 est exclu car donne 421. Avec $ = 2 dans 12$ et 1$2, nous avons 122 et 122 qui ne correspond qu'à un seul lancer (fait du hasard), même si nous avons le choix des deux dés à conserver (mon fait). Il y a six telles configurations à retirer.	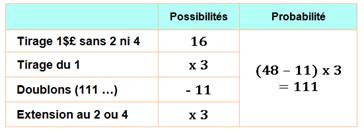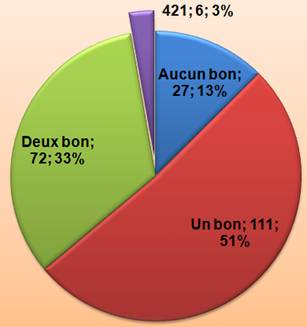Lors d'un lancer la probabilité d'obtenir deux bons numéros du 421 est de 72 chances sur 216.

Un seul bon chiffre au premier lancer
Configuration 1$£ avec ($, £) = {1, 3, 5, 6} donne quatre fois quatre possibilités. Position du 1 en 1$£, $1£ ou$£1 => 3 possibilités. Retirer les doublons lorsque deux 1 ou trois 1 apparaissent. Il y a choix multiple, mais résultant d'un seul lancer (voir le tableau). 111 procure 3 choix, un seul lancer à retenir, deux à rejeter; 113 procure 2 choix pour un seul lancer; un à rejeter trois fois avec $ = {3, 5, 6} et et encore 3 fois selon la place de $. Changement du 1 en 2 ou 4 => 3 possibilités.	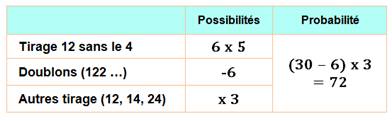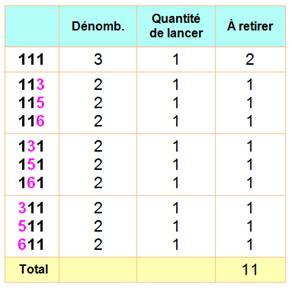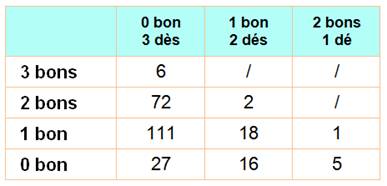Le tableau montre les cas de doublons. Si un lancer donne 111, j'ai trois possibilités pour retenir un seul 1 pour un seul lancer. Mon dénombrement ayant compté tous les cas, je dois exclure deux doublons. Lors d'un lancer la probabilité d'obtenir un seul bon numéro du 421 est de 111 chances sur 216.

Bilan

Lors d'un premier lancer, nous savons qu'il existe 216 possibilités avec: 6 cas pour obtenir 421 du premier coup, 27 cas pour ne rien obtenir du tout, et 183 cas pour obtenir un bon chiffre ou deux bons chiffres dont: 111 cas avec un seul bon numéro, et 72 cas avec deux bons numéros.

Tableau des possibilités pour atteindre 421
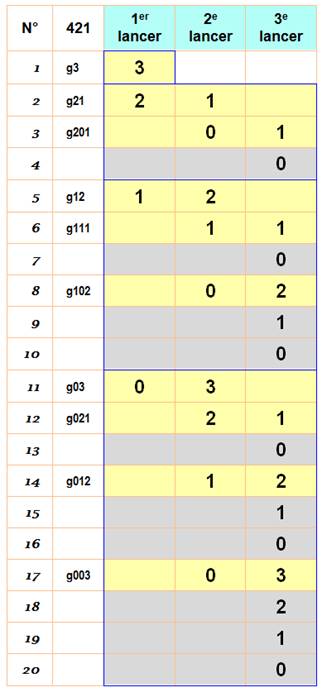
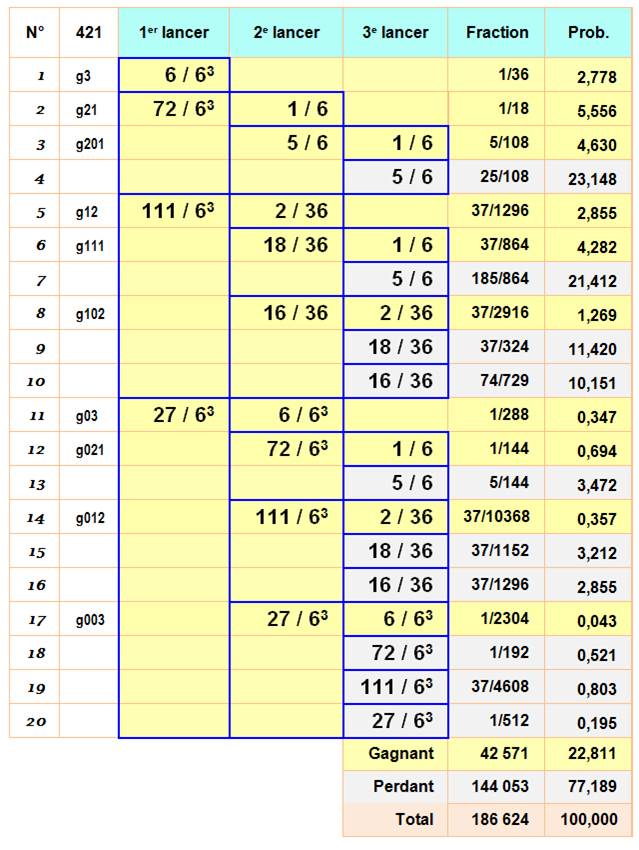
Première possibilité (N°1) La réussite du 421 en un seul lancer est probable avec une chance sur 36 (soit 2,7%); Nous noterons 3 dans la colonne 1^er lancer et nous nommerons g3 ce coup gagnant. Deuxième possibilité (N°2) Le premier lancer montre deux dés gagnants et le troisième est obtenu au deuxième lancer. Ce coup gagnant est noté g21. Troisième possibilité (N°3) Encore deux dés gagnants. Rien au deuxième lancer et le dernier gagnant au troisième lancer. Coup gagnant noté g201. Quatrième possibilité (N°4) Malgré les deux dés gagnants au premier lancer, rien aux lancers suivants. Coup perdant. Etc. Bilan Le tableau montre dix cas gagnants pour dix cas perdants. Reste à savoir avec quelle probabilité se produisent tous ces cas.

Cas G21
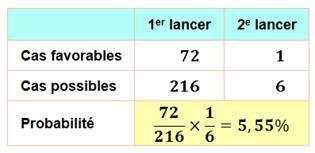
Premier lancer Deux dés gagnants: 72 cas sur 216 Deuxième lancer Reste un seul dé à lancer. Une chance sur six de tomber sur le bon quel qu'il soit du fait des deux chiffres obtenus au premier lancer.	La probabilité de faire 421 en 2 bons puis 1 bon est égale à 5,55%.

Cas G201
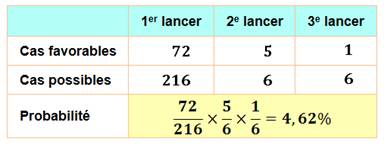
Premier lancer Idem précédent: 72/ 216. Deuxième lancer Cinq chances sur six de rater le 421. Troisième lancer Une chance sur six d'obtenir le chiffre manquant.	La probabilité de faire 421 en 2 bons, rien puis 1 bon est égale à 4,62%.

Cas G12
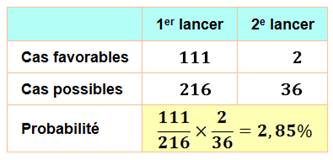
Premier lancer Un des numéros en un seul lancer: 111 cas sur 216 Deuxième lancer Supposons que nous ayons le 1, alors il nous faut 24 ou 42 au second lancer des deux dés. Soit 2 cas sur 36. Avec le 2 et le 4, même résultat. MAIS, nous avons soit le 1, soit le 2, soit le 4 au premier lancer. Dans tous les cas, nous en tenons un et il s'agit de trouver les deux autres au second lancer. Donc 36 (et non pas 3 x 36).	La probabilité de faire 421 en un bon puis deux bons est égale à 2,85%.

Cas G111
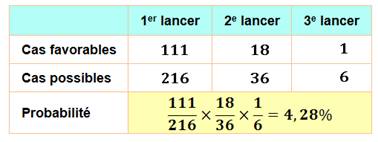
Premier lancer Un des numéros en un seul lancer: 111 cas sur 216 Deuxième lancer Supposons que nous ayons le 1, alors il nous faut 2 ou 4 sur l'un des deux dés. Pour obtenir le 2: 5 possibilité sur chaque dé =>10; Doublon avec 22 => retire 1; Doubler ce compte avec le 4. Soit (10 – 1) x 3 = 18 cas. Troisième lancer Une chance sur 6 d'obtenir le manquant.	La probabilité de faire 421 en un bon puis un bon puis un bon est égale à 4,28%.

Bilan

À ce stade nous pourrions examiner les cas un par un. Mais revoyons nos calculs élémentaires:

Nous pouvons désormais remplir le tableau des probabilités dans chaque cas: ceux déjà calculés et les cas restants.

Tableau des probabilités
Nous avons déjà dressé le tableau des possibilités. Nous connaissons les probabilités pour les lignes gagnantes de g3 à g111. Nous plaçons ces valeurs dans le tableau. Avec les données ci-dessus, il n'est pas très difficile de compléter pour les autres cas. Les fractions indiquées vous montrent la logique du remplissage.

Bilan

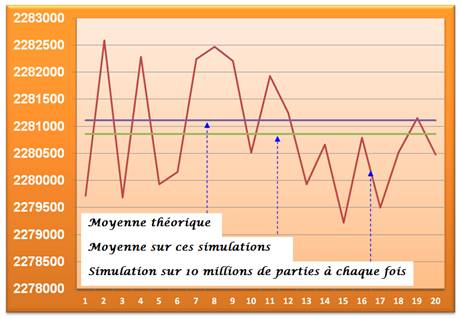
La probabilité d'obtenir 421 en trois lancers est égale à 22,811%.

Ou plus précisément: 42 571 / 186 624.

Simulation
Le jeu du 421 simulé sur ordinateur confirme ce résultat. La programmation est facilitée par le choix des numéros gagnants. En effet, l'addition des bons numéros donne des sommes distinctes: 1 =>1; 2 => 2; 4 => 4; 1 + 2 = 3; 1 + 4 = 5; 2 + 4 = 6; 1 + 2 + 4 = 7. Cette simulation montre comment agit la loi des grands nombres.

Suite	Jeu de dés – Types, probabilité … Jeux et énigmes – Index
Voir	Partage – Énigmes classiques Partage en dix Polygone, Octogone
DicoNombre	Nombre 421
Cette page	http://villemin.gerard.free.fr/aJeux1/Societe/Jeu421.htm