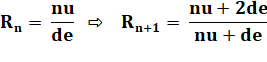|
Édition du: 29/07/2025 |
|
INDEX |
Python – Comment se lancer et initiation |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
PROGRAMMATION PYTHON – Plus de chiffres significatifs Sans autres indications, Python travaille avec 15
chiffres significatifs. Comment calculer Pi ou e avec 100 chiffres
significatifs ou plus ? En appelant le module decimal et en recalculant leurs valeurs. |
||
|
|
Sommaire de cette page Calculs avec
sympy >>>
Valeurs de Pi et e >>>
Valeurs de Racine de 2, de log et d'une fraction >>>
Valeur du nombre d'or et de zêta Algorithmes de
calcul sans sympy >>>
Calcul de 1/7 >>>
Valeurs de Pi et e >>>
Calcul de Racine de 2 >>>
Calcul de Pi et e avec 100 décimales |
Débutants Glossaire |
Voir absolument Mon espace de travail
en Python
|
from sympy import pi, E, N # Afficher Pi avec 100
décimales print("Pi :", N(pi, 101)) # Afficher e avec 100
décimales print("e :", N(E, 101)) |
Pi : 3.14159… e :
2.71828… Voir Toutes les décimales |
|
Voir Comment
calculer Pi et e avec des formules / Constante
Pi / Constante
e
|
from sympy import sqrt, log, Rational, N # Précision : 101 chiffres (100
décimales) precision = 101 # Constantes racine2 = N(sqrt(2), precision) ln2 = N(log(2), precision) inv213 = N(Rational(1, 213), precision) # Affichage print("√2 =", racine2) print("ln(2) =", ln2) print("1/213 =", inv213) |
||
|
√2
= 1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679
7379907324 7846210703 8850387534 3276415727 ln(2) = 0.6931471805 5994530941 7232121458
1765680755 0013436025 5254120680 0094933936 2196969471 5605863326 99641868754 1/213 = 0.0046948356 8075117370 8920187793 4272300469
4835680751 1737089201 8779342723 0046948356 8075117370 8920187793427 |
||
Voir Racine de 2
/ Logarithme
/ Fraction
périodique
|
from sympy import sqrt, N, zeta precision = 101 # Nombre d’or phi = N((1 + sqrt(5)) / 2, precision) # Zêta(3) zeta3 = N(zeta(3), precision) print("ϕ (nombre d’or)
=", phi) print("ζ(3) (zêta de
Riemann en 3) =", zeta3) |
||
|
ϕ (nombre d’or) = 1.6180339887 4989484820 4586834365
6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911375 ζ(3) (zêta de Riemann en 3) = 1.2020569031 5959428539
9738161511 4499907649 8629234049 8881792271 5553418382 0578631309 0186455873 6093352581 |
||
Voir Nombre d'or
/ Zêta de
Riemann
![]()
Algorithmes de calcul sans sympy
|
|
|||
|
Simple calcul de l'inverse de 7
0,142857 142857 142857 142857
14285714 |
Demande d'impression du résultat de la division
1/7. Le programme retourne la valeur avec 17 décimales
justes. On sait que les décimales sont périodiques. En noir, ce que fournit la calculette pour comparaison. |
||
|
On demande à montrer plus de
décimales
|
Cette instruction curieuse affiche plus de
chiffres, mais ils sont faux. |
||
|
Appel au module décimal
ou
ou
ou, enfin
|
On appelle le module decimal
qui manipule de grands nombres en virgule
flottante. Un objet du type Decimal
est crée en utilisant la fonction decimal.Décimal. Notez les majuscules et minuscules. Notez toutes les versions possibles. La deuxième
étant la plus simple. Sans autre précision, le résultat comporte 30
décimales |
||
|
Plus de chiffres
ou
|
Pour plus de chiffres, il suffit de donner la
quantité dans cette instruction dédiée. |
||
|
|
||
|
Calcul normal
3, 141592653589793 2,
718281828459045 |
Appel au module math
qui connait les constantes pi et e Comparaison avec d'autres moyens (calculette,
Maple …) Le résultat est donné avec 15 décimales justes. |
|
|
|
Note: On n'appelle
que la constante Pi. En fait, l'astérisque * joue le rôle de joker
pour appeler tous les membres du module math. |
|
|
Calcul avec module décimal
|
Appel du calcul avec 40 décimales. Mêmes résultats que précédemment. Le module maths ne connait les constantes qu'avec
15 décimales. |
|
|
Pour obtenir plus de décimales, il faut recalculer les constantes ou faire appel à sympy: |
Calcul avec nombreuses décimales
|
|
|
|
|||
|
Accès direct
|
Cette fois Python connait la fonction racine carrée
(sqrt). Appel au module décimal La racine carrée (sqrt)
est une fonction pour laquelle on précise la valeur à calculer en tête (et
non dans les parenthèses). Ici 2, mais on aurait pu mettre toute autre
valeur. Résultat avec 100 décimales. |
||
|
Calcul de la racine de 2
1.4142135623 7309504880 1688724209
6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 327641573 |
Exercice de programmation Python Comment calculer 100 décimales ou plus? Appel au module decimal On nomme D le raccourci de Decimal; tous les
calculs seront dans D(…). Le nombre de décimales est spécifié par nd. La racine est calculée par la formule
itérative:
On se donne une fraction
proche de racine de 2 (nu / de) comme
racine de l'algorithme. L'itération i
est poursuivie un peu au-delà de nd pour
s'assurer que les dernières décimales seront significatives. |
||
|
Calcul complet avec formules donnant Pi et e |
from decimal import Decimal, getcontext # Définir la précision à 110 chiffres (100 décimales + marge) getcontext().prec = 110 def calcul_pi(): # Formule de Machin : π = 16 * arctan(1/5) - 4 * arctan(1/239) def arctan(x): x = Decimal(x) total = x x_squared = x * x term = x i = 1 while True: term *= x_squared next_term = term / (2*i + 1) if next_term == 0: break total += (-1)**i * next_term i += 1 return total pi = 16 * arctan(Decimal(1)/5) - 4 * arctan(Decimal(1)/239) return pi pi_100 = calcul_pi() print("Pi avec 100 décimales :") print(str(pi_100)[:102]) # 1 chiffre
avant la virgule + 100 décimales print(len(str(pi_100))) def calcul_e():# formule avec exponentielle e = Decimal(0) fact = Decimal(1) for i in range(0, 150): # Plus d’itérations pour plus de précision if i > 0: fact *= i e += Decimal(1) / fact return e e_100 = calcul_e() print("\nValeur de e avec 100 décimales :") print(str(e_100)[:102]) print(len(str(e_100))) |
|
|
3.1415926535 8979323846 2643383279
5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 Valeur de e avec 100 décimales : 2.7182818284 5904523536 0287471352
6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 |
||
Voir Calcul de
Pi (Programmes Maple) / Calcul
de e
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette page |
![]()