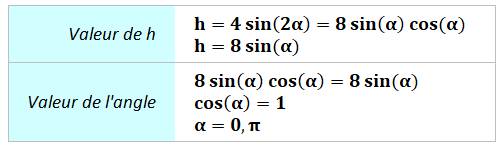énigme du triangle plat

Édition du: 22/07/2023

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Carré et triangle équil.	Triangle plat
	Cercle et demi-cercle	Trapèze et triangle	Triangles dans triangle

Triangle plat ou …

Un défi pathologique. Comment le résoudre ? Deux solutions selon la mesure des côtés.
Le même défi mais avec un résultat plus satisfaisant …

Sommaire de cette page

>>> Le triangle impossible

>>> Le triangle avec inversion des côtés

>>> Le triangle normal – Trigo

>>> Le triangle normal – Géométrie

Débutants

Géométrie

Glossaire

Géométrie

Le triangle impossible			haut
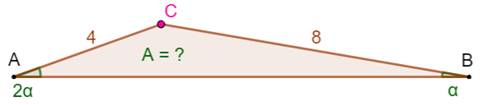
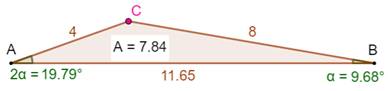
Construction Un triangle ABC dont l'un des angles vaut le double de son voisin. Deux de ses côtés mesurent 4 et 8 cm. Aire du triangle ?
Calculs Voir Relations trigonométriques Conclusion Avec les conditions indiquées, le triangle est dégénéré triangle plat (deux angles nuls).
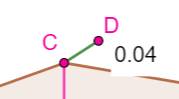
Observations Ce triangle est proche du triangle requis, cependant: Si C est tel que AC = 4 et BC = 8 et D est le point d'intersection des demi-droites d'angle alpha et deux alpha, alors la distance entre les deux est minime, mais égale (ici) à 0,04. En tentant de réduire cette distance, l'angle alpha tend vers zéro.

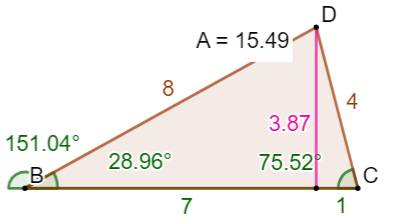
Le triangle avec inversion des côtés		haut
Construction Même chose que ci-dessus en inversant les longueurs des côtés. Piste Cette fois la construction est possible, mais l'angle alpha dépasse 45° et son double dépasse les 90°; de sorte, qu'il faut considérer l'angle supplémentaire (angle moins 180°).
Calculs L'angle alpha vaut 75,52…° et son double 151,04…°. Pour que la construction soit possible, il y a nécessité de prendre son supplément: 180-151,04… = 28,955…

Deux méthodes de résolution pour ce nouveau problème

Le triangle normal – Trigo		haut
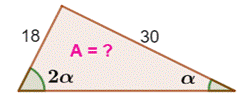
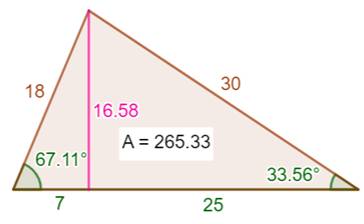
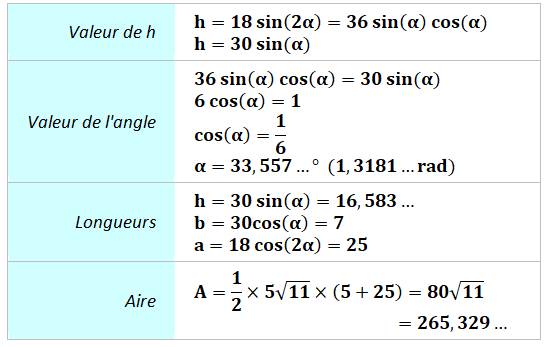
Construction Un triangle ABC dont l'un des angles vaut le double de son voisin. Deux de ses côtés mesurent 18 et 30 cm. Aire du triangle ? Piste Cette fois le calcul se déroule normalement: les angles sont compatibles, et le triangle n'est pas dégénéré.
Résolution par trigonométrie

Le triangle normal – Géométrie		haut
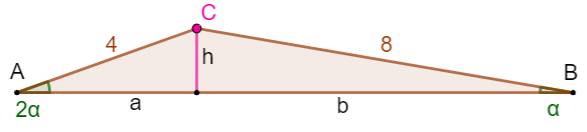
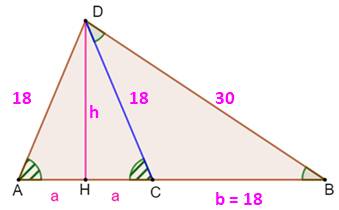
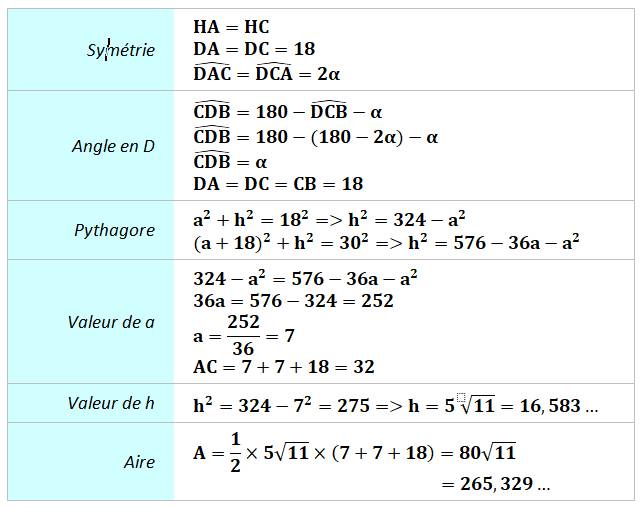
Construction La même que ci-dessus. Trouver l'aire par simple géométrie. Piste Construire DC symétrique de DA par rapport à DH. Alors le triangle DAC est isocèle. Montrer que le triangle CBD l'est aussi. Appliquer le théorème de Pythagore pour trouver les valeurs de a puis de h.
Résolutions par géométrie

Retour

Défis – Index

Géométrie – Index

Énigmes – Index

Brèves – Index

Voir

Cette page